Tronco de pirâmide
O tronco de pirâmide é um sólido geométrico obtido do corte da secção transversal (paralelo a base) de uma pirâmide. Ele é a parte de baixo desse corte:
Note que a base maior e a base menor sempre são compostas por polígonos semelhantes, podendo ser triângulos, quadrados, retângulos, pentágonos, hexágonos ou qualquer outro polígono. Além disso, as faces laterais de um tronco de pirâmide são sempre trapézios.O tronco de pirâmide possui como principais elementos a base menor, a base maior e a altura, que são úteis para o cálculo de seu volume e área total. Vamos conhecer mais?
Para calcular a área lateral total agora, basta multiplicar essa fórmula pela quantidade de lados do tronco:
Onde:
- AREA LATERAL:
Como ja dito, as laterais do tronco são sempre formados por trapézios, no qual, tem sua área calculada pela fórmula:
Para saber mais de trapézio acesse: https://blogdescomplicandomatematica.blogspot.com/2021/10/trapezio.html
Observe que, no caso do tronco, a altura (h) não será a altura do tronco e sim a apótema da lateral, então, a fórmula será escrita da seguinte maneira:
Onde:
B = base maior
b = base menor
Ap = apótema
n = número de lados
Existe, também, um outro jeito de calcular a área lateral, que é através do perímetro da base maior e da base menor, pois, quando multiplicamos o valor da base, seja ela maior ou menor, pelo número de lados, estamos encontrando seu perímetro. Assim, a fórmula também pode ser escrita da seguinte maneira:
2PB = Perímetro da base maior
2Pb = Perímetro da base menor
ap = apótema
Podendo ainda, reduzir a fórmula para o semiperímetro:
Onde;
PB = semiperímetro da base maior
Pb = semiperímetro da base menor
ap = apótema
Exemplo:
Calcule a área lateral de um tronco de pirâmide quadrada que tem como base maior 5cm e base menor 3cm e apótema igual a 4cm.
Pirâmide quadrada = 4 lados.
Podemos calcular assim:

Ou ainda, podemos calcular assim:
Perímetro da Base maior = 5 . 4 = 20cm /2 = 10cm de semiperímetro
Perímetro da Base menor = 3 . 4 = 12cm/2 = 6cm de semiperímetro
- ÁREA TOTAL:
Para cálcular a área total basta somar a área da base maior com a área da base menor com a área lateral.
Atenção: A fórmula da área da base, tanto menor quanto maior, será de acordo com o tipo de pirâmide.
Exemplo:
Qual é a área total de um tronco de pirâmide quadrada que tem como base maior 5cm e base menor 3cm e apótema igual a 4cm.
Área da base maior:
Base quadrada = área do quadrado
AB = l²
AB = 5²
AB = 25cm²
Área da base menor:
Base quadrada = área do quadrado
Ab = l²
Ab = 3²
Ab = 9cm²
Área lateral ja calculamos no exemplo anterior:
At = 25 + 9 + 64 = 98cm²
- VOLUME:
O volume é o espaço em 3 dimensões (largura, altura, comprimento) que o sólido ocupa.
Para calcular o volume do tronco da pirâmide, podemos usar da seguintes fórmulas:
Para saber mais de volume de pirâmide acesse:
Outra fórma de calcular é pela fórmula:
Onde:H = Altura
B = Área da base maior
b = Área da base menor
Mas de onde vem essa fórmula?
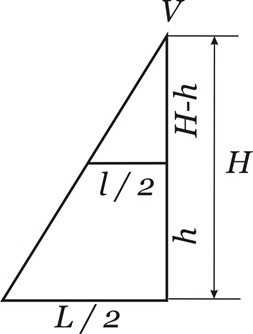
Observe a figura abaixo:
Vamos pegar o triângulo vermelho:
(H-h) está H assim como: l/2 está para L/2. Ou seja, observe que ambos triângulos possuem tamanhos proporcionais um ao outro.
Então, vamos reescrever da seguinte maneira:
Vamos lembrar que l² é a área de um quadrado, então se elevarmos tudo ao quadrado temos:
L² se refere a área da base maior, por isso, foi substituído por AB, e l² se refere a área da base menor, por isso, foi substituído por Ab.
Vamos isolar o H:
Como ja dito, o volume do tronco pode ser calculado pela seguinte fórmula:
ou seja:
Subsituindo o H pelo isolado anteriormente temos:
Exemplo:
Qual é o volume do tronco de uma pirâmide quadrada com base maior igual a 5cm, base menor igual a 2cm e altura igual a 3cm?
Vídeo:
Atividade geogebra: