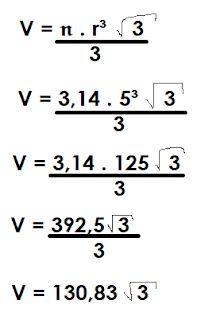Cone equilátero
Quando o diâmetro da base é igual a geratriz do cone, temos um cone equilátero.
A planificação do cone ocorre da seguinte forma:
Os elementos de um cone são:
Geratriz: São os segmentos de retas em um ponto da circunferência até o vértice superior;
Vértice: O cone possui um vértice que fica oposto a base circular.
Eixo de rotação: É a reta que parte do centro da base até o vértice superior; é também o tamanho da reta que define a altura do cone.
ÁREA DA BASE:
Como vimos para calcular a área da base nada mais é do que calcular a área do círculo, logo:
A área lateral, vimos no cone reto que é calculado por:
Como nossa geratriz é igual a 2r, substituindo temos:
Exemplo:
Qual é a área lateral de um cone equilátero de raio igual a 5cm?
Al = 2𝖓r²
Al = 2 . 3,14 . 5²
Al = 2 . 3,14 . 5²
Al = 2 . 3,14 . 25
Al = 157cm²
ÁREA TOTAL:
A área total é a soma das áreas da base com a área lateral.
At = Al + Ab
At = 2𝖓r² + 𝖓r²
At = 3𝖓r²
Exemplo:
Qual é a área total de um cone equilátero de raio igual a 5cm?
At = 3𝖓r²
At = 3 . 3,14 . 5²
At = 3 . 3,14 . 25
At = 235,5cm²
VOLUME:
Volume é o espaço tridimencional que o objeto ocupa.
Como vimos no cone circular reto a fórmula do volume é:
Podemos usar essa fórmula tranquilamente para calular o volume do cone equilátero.
Mas ainda, podemos reduzir ela, pois no caso de cone equilátero, como sabemos a geratriz, podemos usar a relação do triângulo retângulo formado no cone para encontrar a altura. Então observe:
A altura, o raio da base e a geratriz formam um triângulo retângulo, no qual podemos aplicar Pitágoras para encontrar a relação entre elas:
Exemplo:
Qual é o volume do cone equilátero que tem o raio igual a 5cm?
Vídeo:
atividade geogebra:
