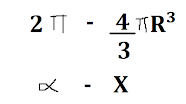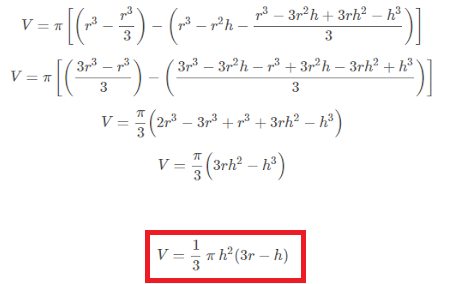Partes da esfera e superfície esférica

Existem partes da esfera que recebem nomes específicos, como o fuso esférico, a cunha esférica, zona esférica e calota esférica. Vamos conhecer cada uma delas?

- FUSO ESFÉRICO (SUPERFÍCIE)

O fuso esférico é a parte da superfície formada pelo giro de uma semicircunferência em graus em torno do diâmetro da esfera.

Um fuso esférico é equivalente a um fuso horário. O fuso horário é a divisão de uma esfera em 24 partes e, assim, configura um fuso esférico formado por uma semicircunferência que girou apenas 15°.

O cálculo dela é simples,  basta usarmos a regra de três simples:

Se a área da esfera é calculada por 4ℼr² tendo o seu angulo total de 360º, quanto será a área do fuso para o ângulo específicado:

360º -   4ℼr²

𝛂      -     x

Podemos realizar o cálculo em radiano, também:

Lembrando que 360º é igual a 2ℼ rad:

  2ℼ     -   4ℼr²

𝛂      -     x

Exemplo:
Qual é a área do fuso esférico de ângulo igual a 15º, cujo o raio da esfera mede10cm?

360º -   4ℼr²

15º   -     x

360x = 15.4ℼ10²

360x = 60ℼ100

360x = 6000ℼ

x = 6000ℼ/360

x = 16,67ℼcm²

- CUNHA ESFÉRICA (VOLUME)

Corresponde à parte da esfera obtida ao girar um semicírculo em torno de seu eixo.

Usamos a regra de três para cálcular o fuso horário que se refere à área dessa parte da esfera. Aqui, também utilizaremos a regra de três, com a diferença de que, nesse caso, o cálculo se refere ao volume.

Como o volume da esfera é calculado por quatro terço do pi multiplicado ao raio elevado ao cubo, e o ângulo da esfera total é de 360º ou 2ℼ rad. Quanto medirá o volume para o ângulo alfa:

ou se radiano:

Exemplo:

Qual é o volume da cunha esférica de ângulo igual a 15º, tendo a esfera raio de 10cm?

- ÁREA DA ZONA ESFÉRICA:

A zona esférica é uma parte da esfera que foi cortada por dois planos paralelos entre si e perpendicularmente ao eixo e rotação da esfera.

Vamos novamente a regra de três:

Se para a altura H temos 2.R e sua área total é calculada por: 4ℼR², quanto será a área para a altura h?

Logo, a área da zona esférica é:

Exemplo:

Qual é a área da zona esférica de raio igual a 10cm e altura igual a 15cm?

Az = 2ℼRh

Az = 2ℼ.10.15

Az = 300ℼcm²

- ÁREA DA CALOTA ESFÉRICA:

Uma calota esférica, em geometria, é a parte de uma esfera cortada por um plano.

A proporção para o cálculo da calota esférica é o mesmo que foi utilizado na zona esférica:

Se para a altura H temos 2.R e sua área total é calculada por: 4ℼR², quanto será a área para a altura h?

Ou seja, a fórmula de área é a mesma:

Exemplo:

Qual é a área da calota esférica de raio igual a 10cm e altura igual a 3cm?

Ac = 2ℼRh

Ac = 2.ℼ.10.3

Ac = 60ℼcm²

- VOLUME DA CALOTA ESFÉRICA:

A fórmula para cálculo do volume da calota é dado por:

Mas de onde vem essa fórmula?

Seguindo a postagem do Baricentro da mente: https://www.obaricentrodamente.com/2010/09/volume-de-uma-calota-esferica.html

Partindo da equação reduzida da circunferência:

Como a esfera tem centro na origem, temos que a = 0 e b = 0, logo:

Vamos supor que a calota esférica é formada por vários cilindros de altura infinitesimais dx e raio y, no qual, o raio muda em cada ponto h:

Sabemos que o volume do cilindro é dado por:

V = Ab. h

V = ℼr² . h

Nesse caso o r é o y e o h é o dx, então:

V = ℼy² . dx

Vamos definir os limites de integração serão de r–h até r.

Então, a soma destes infinitos cilindros de alturas infinitesimais forma a calota esférica será:

O pi é constante, então:

Vamos substituir o valor do y pelo da fórmula da equação reduzida da circunferência:

Integrando em relação a x, obtemos:

Aplicando os limites:

Resolvendo:

Exemplo:

Qual é o volume da calota esférica de raio igual 5cm e altura igual a 8cm?

- VOLUME DA ZONA ESFÉRICA:

É calculado pela fórmula:

Mas de onde vem essa fórmula?

Vamos voltar na fórmula do volume da calota na seguinte expressão:

V = ℼy² . dx

Vamos definir novos limites de integração para esse caso, que serão, pela relação de Pitágoras:

Agora, vamos calcular novamente:

O pi é constante, então:

Vamos substituir o valor do y pelo da fórmula da equação reduzida da circunferência:

Integrando em relação a x, obtemos:

Aplicando os limites:

Observe a seguinte relação ainda:

Então, podemos substituir tudo o que for subtração das raízes de R² -r1² por R² - r2² por h:

Precisamos achar uma relação para o produto das raízes, vamos usar a seguinte relação e elevar o h ao quadrado:

Vamos substituir na fórmula:

Vamos colocar novamente o pi vezes h dividido por 3 em evidência:

vídeo:

Atividade geogebra: