Propriedade de um Poliedro convexo e relação de Euler
Um poliedro será convexo quando for formado por polígonos convexos, de forma que as condições a seguir sejam aceitas:
- Dois dos polígonos nunca são coplanares, ou seja, não pertencem ao mesmo plano.
- Cada lado de um desses polígonos pertence a apenas dois polígonos.
- O plano que contém qualquer um desses polígonos deixa os demais polígonos no mesmo semiespaço.
Propriedade 1
A soma das arestas de todas as faces é igual ao dobro do número de arestas do poliedro.
Exemplo:
Um poliedro tem 6 faces quadradas. Vamos determinar a quantidade de arestas.
De acordo com a propriedade, basta multiplicar o número de arestas de uma face pela quantidade de faces, e isso é igual ao dobro do número de arestas. Dessa forma:
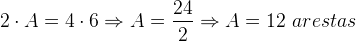
Propriedade 2
A soma dos vértices de todas as faces é igual à soma das arestas de todas as faces, que é igual ao dobro do número de arestas.
Exemplo:
Um poliedro com 5 ângulos tetraédricos e 4 ângulos hexaédricos. Vamos determinar a quantidade de arestas.
De maneira análoga ao exemplo anterior, a segunda propriedade diz que a soma das arestas de todas as faces é igual ao dobro do número de arestas. O número de arestas é dado pelo produto de 5 por 4 e 4 por 6, pois são 5 ângulos tetraédricos e 4 hexaédricos. Assim:
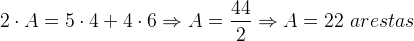
Onde:
Leonhard Euler (1707-1783) foi um importante matemático e cientista suíço, foi considerado um dos maiores estudiosos da matemática, em sua época. Sua contribuição teve como um dos pilares a Introdução à Análise dos Infinitos, obra que constitui um dos fundamentos da matemática moderna.
A relação criada pelo matemático suíço Leonhard Euler possui extrema importância na determinação do número de arestas, vértices e faces de qualquer poliedro convexo e de alguns não convexos.
1 - Determine o número de faces de um sólido que apresenta 10 arestas e 6 vértices.
Resolução:
V – A + F = 2
6 – 10 + F = 2
–4 + F = 2
F = 4 + 2
F = 6
O sólido possui, portanto, 6 faces.
2 - Determine o número de arestas de um sólido geométrico que possui 10 vértices e 7 faces.
V – A + F = 2
10 – A + 7 = 2
– A = 2 – 7 – 10
– A = – 15
A = 15
O sólido possui 15 arestas.
3 - Determine o número de vértices da pirâmide quadrangular a seguir:
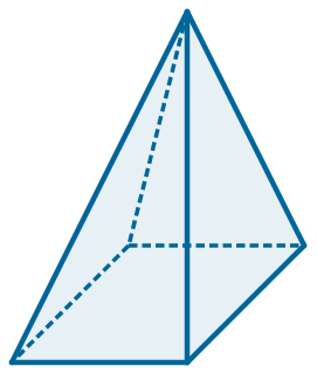
Visivelmente, podemos afirmar que a pirâmide apresenta 5 vértices, 5 faces e 8 arestas. Vamos, agora, demonstrar que a relação de Euler é válida para determinar esses elementos da pirâmide de base quadrangular.
Resolução:
Vértices
V – A + F = 2
V – 8 + 5 = 2
V = 2 + 3
V = 5
- Dois dos polígonos nunca são coplanares, ou seja, não pertencem ao mesmo plano.
- Cada lado de um desses polígonos pertence a apenas dois polígonos.
- O plano que contém qualquer um desses polígonos deixa os demais polígonos no mesmo semiespaço.
Propriedades de um poliedro convexo
Propriedade 1
A soma das arestas de todas as faces é igual ao dobro do número de arestas do poliedro.
Exemplo:
Um poliedro tem 6 faces quadradas. Vamos determinar a quantidade de arestas.
De acordo com a propriedade, basta multiplicar o número de arestas de uma face pela quantidade de faces, e isso é igual ao dobro do número de arestas. Dessa forma:
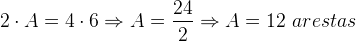
Propriedade 2
A soma dos vértices de todas as faces é igual à soma das arestas de todas as faces, que é igual ao dobro do número de arestas.
Exemplo:
Um poliedro com 5 ângulos tetraédricos e 4 ângulos hexaédricos. Vamos determinar a quantidade de arestas.
De maneira análoga ao exemplo anterior, a segunda propriedade diz que a soma das arestas de todas as faces é igual ao dobro do número de arestas. O número de arestas é dado pelo produto de 5 por 4 e 4 por 6, pois são 5 ângulos tetraédricos e 4 hexaédricos. Assim:
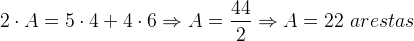
Relação de Euler
A relação de Euler é usada para relacionar o número de faces, vértices e arestas de poliedros convexos. Assim, ela pode facilitar a contagem desses elementos. Essa relação é dada pela seguinte expressão:
V – A + F = 2
Onde:
V é o número de vértices,
A é o número de arestas e
F é o número de faces do poliedro.
A relação criada pelo matemático suíço Leonhard Euler possui extrema importância na determinação do número de arestas, vértices e faces de qualquer poliedro convexo e de alguns não convexos.
Exemplo de aplicação:
Resolução:
V – A + F = 2
6 – 10 + F = 2
–4 + F = 2
F = 4 + 2
F = 6
O sólido possui, portanto, 6 faces.
V – A + F = 2
10 – A + 7 = 2
– A = 2 – 7 – 10
– A = – 15
A = 15
O sólido possui 15 arestas.
3 - Determine o número de vértices da pirâmide quadrangular a seguir:

Visivelmente, podemos afirmar que a pirâmide apresenta 5 vértices, 5 faces e 8 arestas. Vamos, agora, demonstrar que a relação de Euler é válida para determinar esses elementos da pirâmide de base quadrangular.
Resolução:
Vértices
V – A + F = 2
V = 2 + 3
V = 5
Arestas
V – A + F = 2
5 – A + 5 = 2
–A = 2 – 10
–A = –8 x(–1)
A = 8
V – A + F = 2
5 – A + 5 = 2
–A = 2 – 10
–A = –8 x(–1)
A = 8
Faces
V – A + F = 2
5 – 8 + F = 2
–3 + F = 2
F = 2 + 3
F = 5
Assim, podemos notar que a relação de Euler é realmente válida na determinação dos elementos de um sólido convexo.
V – A + F = 2
5 – 8 + F = 2
–3 + F = 2
F = 2 + 3
F = 5
Assim, podemos notar que a relação de Euler é realmente válida na determinação dos elementos de um sólido convexo.
O teorema surgiu de analises de poliedros, tendo sido descoberto em 1758, porém logo em seguida foi verificado que nem todos os poliedros trabalham conforme a relação, só foi verificado a relação em poliedros convexos e alguns não convexos.
Exemplo:
V – A + F = 2
16 - 32 + 16 = 2
0 = 2
Aqui não funciona pois zero é diferente de 2 e não igual como diz a relação.
vídeo:





