Poliedros - Partes e classificação
Formas tridimensionais são chamadas como sólidos geometricos na geometria espacial, quando esses sólidos são formados por APENAS poligonos planos, temos os Poliedros.
A junção entre faces é o que chamamos de aresta, as faces são os poligonos planos e as quinas dos poliedros são os vértices:Observação:A palavra poliedro vem do grego antigo, poli significa várias e edros significa faces.
Como os Poliedros são classificados
Os Poliedros podem ser classificados como côncavos e convexos.
Côncavo: Se ao traçarmos uma reta entre pontas de um poliedro existir alguma aresta fora dela, temos poliedro côncavo.
exemplo:
Convexo: Se qualquer segmento de reta que liga dois pontos de um poliedro estiver totalmente contido nele, então ele será convexo.
O termo figura convexa refere-se à figuras que apresentam um ângulo menor que um raso. Ou seja, são figuras arredondadas por fora, de maneira curva. Sendo assim, um poliedro convexo é formados por polígonos convexos.Exemplo:
Assim, para que um poliedro convexo se forme, são necessárias algumas determinações como:
- Os dois polígonos que formam um poliedro convexo não pode estar no mesmo plano de um outro polígono, ou seja, não podem ser coplanares;
- Os lados que formam os polígonos devem pertencer apenas à dois polígonos;
- Cada plano de uma face deixa os demais polígonos das outras faces no mesmo semi-espaço;
Poliedros Regulares - Um poliedro convexo é chamado de regular se suas faces são polígonos regulares, cada um com o mesmo número de lados e, para todo vértice, converge um mesmo número de arestas.
Existem apenas cinco poliedros regulares convexos, que são também chamados de “Sólidos Platônicos” ou “Poliedros de Platão”. São eles: tetraedro, hexaedro (cubo), octaedro, dodecaedro, icosaedro.Para que possa ser um poliedro de Platão, é necessário que o poliedro obedeça às seguintes disposições:
a) todas as faces devem ter a mesma quantidade n de arestas;
b) todos os vértices devem ser formados pela mesma quantidade m de arestas;
c) a Relação de Euler deve valer: V – A + F = 2, em que V é o número de vértices, A é o número de arestas e F é o número de faces. (Veremos isso em outra postagem).
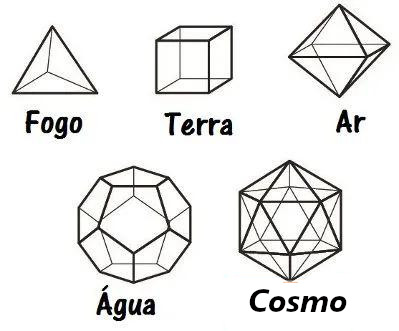
Conta-se que Platão, que, além de matemático, era também filósofo, relacionava esses sólidos geométricos com a construção do Universo, associando o tetraedro ao fogo, o cubo a terra, o octaedro ao ar, o icosaedro à água e o dodecaedro ao Cosmos. Platão acreditava que foi a partir da combinação desses elementos que o Universo foi feito.
Atividade Geogebra:









