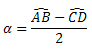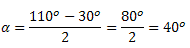Ângulos na circunferência
Existem possibilidades e relações entre os angulos e circuferencia. Cada caso, possui uma propriedade, e o seu estudo é muito importante na geometria, que pode ser vista a seguir:
Ângulo Central:
seu vértice está no centro da circunferência.
Propriedade: o ângulo central apresenta a mesma medida do arco formado por seus lados, ou seja:
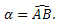
Exemplo:
α = AB
α = 80º
Ângulo inscrito:
seu vértice é um ponto da circunferência.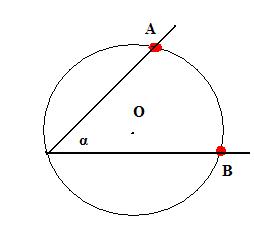
Propriedade: a medida do ângulo inscrito equivale à metade da medida do arco formado por seus lados, ou seja:
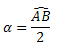
Exemplo:
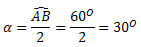
Ângulo de Segmento:
formado por uma corda e uma tangente (com vértice no ponto de tangência).
Propriedade: a medida do ângulo inscrito equivale à metade da medida do arco formado por seus lados, ou seja:
Exemplo:
Determine o valor de α sabendo que o arco AB mede 80º.
Seu vértice é um ponto da circunferência e uma das pontas faz um angulo de 90º quando ligada a outra ponta (forma um triâgulo retângulo).
Ângulo excêntrico interno:
formado por duas cordas. O ângulo do vértice se encontra no interior na circunferência.
Propriedade: o ângulo excêntrico interno possui medida igual à metade da soma dos arcos formados pelos seus lados, ou seja:
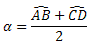
Exemplo:
Determine o valor de α na figura abaixo.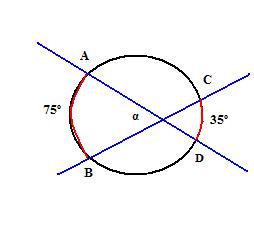
Solução:
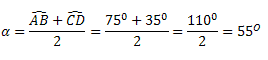
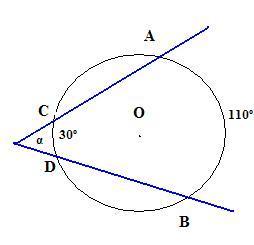
Ângulo Excêntrico Externo:
formado por duas retas secantes à circunferência. O ângulo do vértice se encontra na parte de fora da circunferência.
Propriedade: o ângulo α equivale à metade da diferença entre as medidas dos arcos formados pelos seus lados, ou seja:
Exemplo: Determine o valor de α na figura abaixo.
Para conhecer mais sobre os elementos da circunferência acesse: https://didaticursos.blogspot.com/2021/12/elementos-da-circunferencia.html
Atividade geogebra ângulo excêntrico interno:
