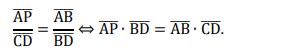Propriedade dos quadriláteros - soma dos ângulos, teorema de Pitot e Ptolomeu-Hiparco
Os quadriláteros podem ser convexos ou côncavos. Um quadrilátero é convexo quando a reta que une dois vértices consecutivos não encontra o lado formado pelos dois outros vértices, conforme figura abaixo;
Já quando a extensão da reta encontra outra reta, temos o quadrilátero côncavo conforma figura abaixo:
Podemos dizer que um quadrilátero está inscrito em uma circunferência, quando todos os 4 vértices desse polígono de 4 lados tocam o seu segmento.
Para que um quadrilátero possa ser inscrito a uma circunferência, os seus ângulos opostos devem, necessariamente, ser suplementares. De outra forma, ou seja, sem atender a essa condição, não haveria como inscrever um polígono de 4 lados em uma circunferência. E dois ângulos são suplementares quando sua soma é igual a 180º, logo:
𝛂 + 𝛄 = 180
Exemplo: Considere o quadrilátero ABCD inscrito numa circunferência, como mostra a figura.
Sabendo que a diagonal AC mede 12 cm, determine a medida da diagonal BD.
Pelo teorema de Ptolomeu, temos que:
AC∙BD = AB∙CD + AD∙BC
Segue que:
Além de suas contribuições na astronomia e na geografia, Ptolomeu influenciou a matemática (em particular, a trigonometria) propondo um teorema que leva seu nome: Teorema de Ptolomeu. Vejamos o que diz esse teorema.
Comprovação do teorema de Pitot:
Quadrilátero côncavo
A soma dos ângulos internos de um quadrilátero convexo é:
observe a figura abaixo:
Observe que podemos cortar o quadrilátero em 2 triângulos e sabemos que a soma do ângulos internos do triângulo é 180º
Logo temos:
a + b1 + d1 = 180º
c + b2 + d2 = 180º
Somando tudo temos:
a + b1 + b2 + c + d1 + d2 = 180 + 180
a + b + c + d = 360º
Com isso sabemos que a soma dos ângulos internos de um quadrilátero é 360º.
Podemos inscrever o quadrilátero em um círculo:
Para que um quadrilátero possa ser inscrito a uma circunferência, os seus ângulos opostos devem, necessariamente, ser suplementares. De outra forma, ou seja, sem atender a essa condição, não haveria como inscrever um polígono de 4 lados em uma circunferência. E dois ângulos são suplementares quando sua soma é igual a 180º, logo:
Ângulo de A + Ângulo de C = Ângulo de B + Ângulo de D = 180º
Exemplo:
Qual é o valor do ângulo 𝛄?
70 + 𝛄 = 180
𝛄 = 180 - 70
𝛄 = 110º
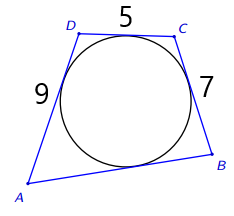
Exemplo. Calcular a medida de AB.
Observe que ABCD é um quadrilátero convexo circunscritível, ou seja, é possível aplicar o teorema de Pitot.
AB + CD = BC + DA
AB + 5 = 7 + 9
AB = 16 – 5
AB = 11
Teorema de Pitot
O teorema de Pitot, que leva o nome do engenheiro francês Henri Pitot, afirma que em um quadrilátero convexo circunscritível o resultado da soma dos comprimentos dos lados opostos é o mesmo.ou seja:
a + c = b + d
Exemplo. Calcular a medida de AB.
AB + CD = BC + DA
AB + 5 = 7 + 9
AB = 16 – 5
AB = 11
CURIOSIDADE: O teorema de Pitot leva o nome do engenheiro francês Henri Pitot (1695- 1771). Começou os seus estudos em matemáticas e astronomia em Paris, tendo-se tornado assistente do eminente físico Réaumur em 1723. Em 1724 foi nomeado membro da Academia das Ciências de França.
Inventou um instrumento para medir a velocidade dos fluidos e que é conhecido hoje pelo seu nome, o tubo de Pitot ainda empregue, nomeadamente, na aeronáutica.
Publicou vários trabalhos sobre estruturas, hidráulica, matemática e saneamento.
Desenvolveu investigações científicas sobre as bombas e o rendimento das máquinas hidráulicas que constituíram importantes contribuições para a hidrodinâmica e a termodinâmica.
Inventou um instrumento para medir a velocidade dos fluidos e que é conhecido hoje pelo seu nome, o tubo de Pitot ainda empregue, nomeadamente, na aeronáutica.
Publicou vários trabalhos sobre estruturas, hidráulica, matemática e saneamento.
Desenvolveu investigações científicas sobre as bombas e o rendimento das máquinas hidráulicas que constituíram importantes contribuições para a hidrodinâmica e a termodinâmica.
Teorema de Ptolomeu-Hiparco
Seja o quadrilátero abaixo inscrito no circulo de laterais a, b, c e d e diagonais m e n. Então:
m . n = a . c + b . d
ou, de outra forma:
AC . BD = AB . DC + AD . BC
DEDUÇÃO - de onde vem a fórmula:
Observe a figura abaixo:
Traçamos uma reta BP, onde AB̂P ≡ DB̂C.
Como BÂC ≡ BD̂C e AB̂D ≡ PB̂C, tem-se,
pelo caso de semelhança, temos as seguintes razões:
E ainda temos as razoes:
Somando as duas temos:
Exemplo: Considere o quadrilátero ABCD inscrito numa circunferência, como mostra a figura.
Sabendo que a diagonal AC mede 12 cm, determine a medida da diagonal BD.
Pelo teorema de Ptolomeu, temos que:
AC∙BD = AB∙CD + AD∙BC
Segue que:
CURIOSIDADE:
Claudius Ptolomeu também foi um desses grandes matemáticos, além de astrônomo e geógrafo. Ptolomeu nasceu por volta do ano de 85 no Egito e morreu, aproximadamente, no ano de 165 em Alexandria, também no Egito. Foi Ptolomeu quem propôs a teoria do geocentrismo, que perdurou por cerca de 1400 anos.Além de suas contribuições na astronomia e na geografia, Ptolomeu influenciou a matemática (em particular, a trigonometria) propondo um teorema que leva seu nome: Teorema de Ptolomeu. Vejamos o que diz esse teorema.
vídeos:
Comprovação que a soma dos angulos internos de um quadrilátero é 360º
Comprovação que a soma dos angulos opostos do quadrilátero inscrito em um circulo é igual a 180º
Demonstração do Teorema de Ptolomeu-Hiparco
atividade geogebra:
