Losango

É o quadrilátero que apresenta os quatro lados iguais. As diagonais são perpendiculares entre si e cortam-se no ponto médio. Ele também é um paralelogramo.

A característica que diferencia os losangos dos outros quadriláteros é que todos os seus lados possuem a mesma medida. Essa figura faz parte da bandeira do Brasil, sendo a figura amarela da bandeira.

Os losangos são compostos por:

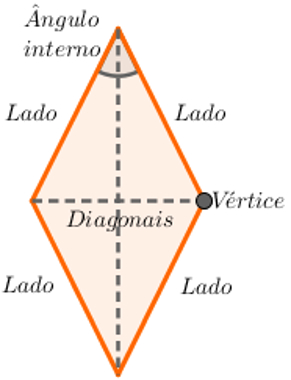
Lados: Cada lado de um polígono é um dos segmentos de reta que determinam seu contorno. Os losangos possuem quatro lados com a mesma medida;

Vértices: São os pontos de encontro dos lados de um polígono e só ocorrem nas extremidades dos lados. Uma figura que apresenta lados que se encontram em outros pontos não é um polígono. O losango possui quatro vértices;

Ângulos internos: São os ângulos formados pelos pontos interiores de um polígono entre dois lados consecutivos. Os losangos possuem quatro ângulos internos e, por serem quadriláteros, a soma desses ângulos sempre é igual a 360°;

Diagonais: São segmentos de reta que ligam dois vértices de um polígono e que, ao mesmo tempo, não são lados dele. O losango apresenta apenas duas diagonais.

Os losangos possuem todas as propriedades dos paralelogramos, a saber:
- Lados opostos são congruentes, ou seja, possuem a mesma forma e tamanho.
- Ângulos opostos são congruentes, ou seja, possuem a mesma medida.
- Ângulos adjacentes são suplementares (ângulos cuja soma resulta em 180°), ou seja, dois ângulos somados um ao lado do outro tem como resultado 180º.

Observe que no caso acima, se somarmos 126,87º + 53,13º = 180º

- As diagonais encontram-se em seus pontos médios.

- As diagonais de um losango são perpendiculares entre si: Essa propriedade também pode ser usada para caracterizar uma figura como losango. Se a figura é um quadrilátero cujas diagonais são perpendiculares (o ângulo entre elas é 90°), então, essa figura é um losango.

Os principais cálculos referentes a essa figura são:

Perímetro:

O perímetro nada mais é do que o contorno da figura, logo o perímetro é calculado como:

Perímetro = L1 + L2 + L3 + L4

Como os lados são todos iguais e se repetem 4 vezes podemos, também, calcular o perímetro como:

Perímetro = 4 . lado

P = 4L

Exemplo:

Qual é o perímetro do losango com lado de 5cm?

P = 4 . l

P = 4. 5

P = 20cm

Área:

A área do losango é o espaço que a figura ocupa. Como o losango é uma figura que não possui base, não é possível utilizar a fórmula do retângulo nele de base x altura.

Vamos analisar a figura: