Inequação modular
Inequações, como já vimos em outra postagem, são expressões que envolvem desigualdade, ou seja, não possui sinal de igual e sim maior, menor, maior e igual e menor e igual. Já modular é quando o número esta entre módulo | | e é a distância entre o número e o zero, por isso dizemos que o módulo nunca é negativo.
Para saber mais de inequação acesse: https://didaticursos.blogspot.com/2021/01/inequacoes-introducao.html
São exemplos de inequação modular:
|x+1| < -5
6 ≤ |2 - x|
Para encontrar o módulo de um número, é necessário seguir a seguinte regra:
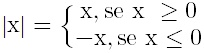
Visto isso, vamos voltar a inequação:
|x| > 2
Aplicando a regra temos
x >2
Ou o número de dentro do modulo, nesse caso o x, ainda pode ser negativo:
-x > 2
Nesse caso, para não deixar a incógnita negativa vamos multiplicar tudo por (-1), então temos:
x < -2
Lembre-se que o sinal de desigualdade também se altera na multiplicação por -1.
Sabendo dessas 2 desigualdade então podemos dizer que
x > 2 ou x < -2
|x| > 2
-2 > x > 2
Observe que usamos a mesma inequação colocando no lado oposto o mesmo sinal de desigual com o sinal do valor trocado (antes era 2 o outro lado da desigualdade ficou -2).
Ambas geram o mesmo gráfico de resposta:
x > 2 ou x < -2
-2 > x > 2
___________________________________________________________________________________
Vamos ao segundo exemplo:
|x+1| < -5
Aplicando a regra temos:
x + 1 < -5
Resolvendo:
x < -5 - 1
x < -6
Ou o número de dentro do módulo, nesse caso (x + 1) ainda pode ser negativo como já vimos:
-x - (+1) <-5
-x - 1 < -5
-x < -5 + 1
-x < -4
Para não o x negativo, vamos multiplicar tudo por -1 temos:
x > 4
então nesse caso temos que x < -6 ou x > 4
Com isso podemos montar o cálculo de inequação da seguinte maneira quando nos deparamos com ela:
|x+1| < -5
5 < x + 1 < -5
Aqui temos que isolar o x passando o 1 para depois de ambos os sinais de desigualdade:
5 - 1 < x < -5 - 1
4 < x < -6
Ambas geram o mesmo gráfico de resposta:
x < -6 ou x > 4
4 < x < -6
___________________________________________________________________________________
Outro exemplo:
6 ≤ |2 - x|
Temos então:
6 ≤ 2 - x
Isolando o x:
6 - 2 ≤ - x
4 ≤ - x
multiplicando tudo por menos 1 para que o x não fique negativo temos:
- 4 ≥ x
ou ainda podemos ter os valores de dentro do módulo negativo:
6 ≤ - (2) - (-x)
6 ≤ - 2 + x
6 + 2 ≤ x
8 ≤ x
Logo - 4 ≥ x ou 8 ≤ x
Com isso podemos montar o cálculo de inequação da seguinte maneira quando nos deparamos com ela:
6 ≤ |2 - x|
6 ≤ 2 - x ≤ -6
Para isolar o x o 2 tem que ir para os dois lados do sinal de desigualdade com sinal trocado:
6 - 2 ≤ - x ≤ -6 - 2
4 ≤ - x ≤ -8
Multiplicando tudo por -1 para não deixar o x negativo, temos:
-4 ≤ x ≤ 8
Ambas geram o mesmo gráfico de resposta:
- 4 ≥ x ou 8 ≤ x
-4 ≤ x ≤ 8
Vídeo:







