Área de um Triângulo

Área é um conceito matemático que pode ser definida como quantidade de espaço bidimensional, ou seja, de superfície. Sua unidade mais comumente usada é o metro quadrado (m²) e seus múltiplos e submúltiplos  (centímetro quadrado - cm², decímetro quadrado - dm², quilometro quadrado - km²).

Existem algumas formas de calcular a área de triângulos, vamos conhecer elas:

O triângulo é o polígono mais simples que existe, porém isso não diminui a importância dele, já que pode ser muito explorado em diversas áreas da matemática e também da física. Embora existam algumas fórmulas diferentes para triângulos equiláteros e retângulos, o cálculo da área de um triângulo qualquer necessita basicamente conhecer o valor da base (b) e da altura (h).

Vamos pensar num retângulo e no conceito de multiplicação:

Ao analisarmos esse retângulo vemos que a área dele é apenas um conceito simples de multiplicação, se tenho 3 unidades de lateral e elas se repetem 5 vezes teremos um total de 15 unidades ou seja:

 3 x 5 = 15. Por isso nesse caso o conceito de base vezes altura para calcular a área.

Fácil, fácil o cálculo de área de um retângulo, agora vamos lembrar que um triângulo nada mais é do que a metade de um retângulo, ou seja, o retângulo é a soma de 2 triângulos:

Logo se o cálculo da área do retângulo é base x altura, a área de um triângulo será:

onde:
A→ área
b → base
h→ altura

Exemplo de uso:

Calcule a área do triângulo a seguir:

ÁREA DE UM TRIÂNGULO COM CÍRCULO INSCRITO

Existe também, uma outra forma de calcular a área de um triângulo, vamos desenhar um circulo inscrito nesse triângulo (dentro dele) e encontrar o raio desse circulo (incentro). Você pode conhecer mais sobre incentro acessando: https://didaticursos.blogspot.com/2021/07/pontos-notaveis-em-um-triangulo.html#more 

Aqui percebemos que o triângulo maior se divide em 3 triângulos menores.

Observe que a altura desses triângulos menores é o raio do circulo inscrito do triângulo.

Se aplicarmos a regra de base vezes altura para cada um dos três triângulos menores teremos:

Sabemos, também, que a área do triângulo maior é a soma das 3 áreas do triangulo:

Área total do triângulo  = Área do triangulo amarelo + Área do triângulo azul + Área do triângulo verde

Logo, temos:

Aqui, como o raio (r) se repete em todas as somas, podemos colocar o r em evidencia, ficando:

No entanto, podemos lembrar que a + b + c é o perímetro de um triangulo, ou seja a soma de todo o contorno do triangulo, então a formula poderia ser escrita da seguinte maneira:

Mas ainda, podemos simplificar ela, chamando o semiperímetro do triângulo que é a metade do perímetro ou seja (a + b + c) /2. Chamando o semiperímetro de p temos a seguinte formula para a área:

A = r . p

onde:

A = área

r = raio

p = semiperímetro.

Exemplo de uso:

Quanto mede a área do triângulo abaixo?

Observe que temos o semiperímetro do triângulo que é a metade do perímetro como sendo:

p = 6 + 6 + 8 = 20

r = 4

logo, aplicando a fórmula temos:

A = r . p

A = 4 . 20

A = 80.

ÁREA DE UM TRIÂNGULO COM SENO DO ÂNGULO

Podemos também calcular a área de um triângulo levando em consideração o seno de um de seus ângulos:

Vamos pegar nosso triângulo e traçar nossa reta de altura dele com base em uma vértice.

O ponto gerado dessa reta altura (h) no segmento AC chamaremos de H.

Observe que foi obtido 2 triângulos desse triângulo ABC - o triângulo AHB e BHC.

Vamos usar o triângulo AHB para calcular o seno de alfa.

o seno é calculado através da fórmula: cateto oposto dividido pela hipotenusa. Com isso, nesse triângulo temos:

h = cateto oposto

c =  hipotenusa.

Lembrando que estamos nos referindo ao triangulo AHB. Então:

Vamos isolar a altura (h):

Vamos agora voltar para aquela nossa fórmula base de área de triângulo em que:

Podemos fazer o mesmo processo para o seno de gama:

Pegando o triângulo BHC teremos:

h = cateto oposto

a = hipotenusa

Logo:

Substituindo na fórmula temos:

Seguindo a lógica  das áreas com sen𝛂 e sen𝛄 temos para sen𝛃:

Resumindo:

Exemplo:

calcular a área do seguinte triângulo: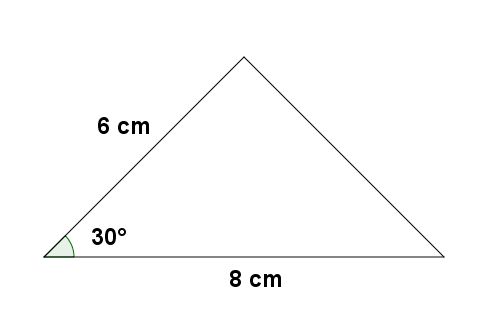

ÁREA DE UM TRIÂNGULO COM CIRCULO CIRCUNSCRITO

Outra forma de calcular a área é através de um circulo circunscrito no triângulo (traçado na parte externa do triângulo).

Através do circuncentro podemos traçar um circulo circunscrito no triângulo (para saber mais acesse: https://didaticursos.blogspot.com/2021/07/pontos-notaveis-em-um-triangulo.html#more).

Observe que nesse triângulo ABC o O é nosso circuncentro.

Traçando uma reta do nosso vértice B passando pelo ponto O até o circulo circunscrito, geramos o ponto D, assim, temos um novo triângulo BDC:

Observe que o ponto C no triângulo BDC passa a ser de 90º e que a reta BD possui o valor de 2 vezes o raio do circulo.

BD = 2r

Vamos trabalhar com os 2 triângulos que aparecem: ABH e BDC

Como esses triângulos são semelhantes:

Podemos fazer a seguinte relação:

onde:

BC = a

BD = 2r

BH = h

BA = c

logo:

Multiplicando cruzado temos:

a . c = 2r . h

Isolando o h temos:

Agora usando a fórmula padrão da área do triangulo de:

Vamos substituir no lugar do h o valor encontrado anteriormente:

Exemplo:

Calcule a área do triângulo abaixo:

ÁREA DE UM TRIANGULO COM SEMIPERIMETRO - FORMULA DE HERON (HERÃO)

Também podemos calcular a área do triângulo conhecendo suas medidas dos lados, através do teorema de Heron que diz o seguinte:

"Se um triângulo possui os lados medindo a, b e c e seu perímetro é indicado por 2p = a + b + c, então sua área triangular é dada por:

"

Heron de Alexandria é o responsável por elaborar uma fórmula matemática que calcula a área de um triângulo em função das medidas dos seus três lados. A fórmula de Heron de Alexandria é muito útil nos casos em que não sabemos a altura do triângulo, mas temos a medida dos lados.

Vamos lá ver de onde vem essa fórmula:

Vamos analisar um triângulo cortando a altura dele pela reta h:

Observe que a reta b se divide com a reta h em x e (b - x - a reta b menos a reta x do lado esquerdo).

O triângulo ABC gera dois triângulos menores com a reta h o ABH e o BCH, com isso podemos aplicar Pitágoras nos 2 triângulos:

ABH:

c² = h² + x²

que isolando o x temos:

x² = c² - h²

x = √c² - h²

BCH:

a² = h² + (b-x)² --

 (b-x)² é o quadrado da diferença logo podemos calcular:

a² = h² + (b² - 2bx + x²)

a² = h² + b² - 2bx + x²

no primeiro triângulo isolamos um valor para x, então podemos pegar esse valor e substituir na ultima expressão:

a² = h² + b² - 2.b.(√c² - h²) + (√c² - h²)²

Potência de raiz se anulam... logo:

a² = h² + b² - 2.b.(√c² - h²) + c² - h²

Podemos calcular o que podemos ficando:

a² = b² - 2.b.(√c² - h²) + c²

Vamos isolar o h²:

a² - b² - c² =  - 2.b.(√c² - h²)

Como sabemos a área de um triângulo é (base vezes altura) dividido por 2:

substituindo a altura ao quadrado pelo h² já isolado anteriormente temos:

Para compreender o que vamos fazer a seguir, vamos chamar o (2bc) de z e o (b² + c² - a²) de y, então temos:

Podemos reescrever o z² - y² da seguinte maneira fatorada:

(z + y) . (z - y)  tudo isso utilizando a multiplicação será igual a z² - y².

Logo podemos reescrever a formula como:

Agora voltando aos valores corretos de que foi mudado para z e y teremos:

Vamos agora, chamar (b + c) de s e (b - c) de k, para podermos aplicar novamente a fatoração, pois temos o quadrado de 2 termos:

Fatorando teremos:

Agora voltando os valores normais que foram  substituídos por s e k teremos:

Vamos lembrar que (a + b + c)/2 nada mais é do que o semiperímetro (p) do triângulo, e esta aparecendo na primeira multiplicação, teremos então:

Para as outras 3 partes multiplicadas vamos analisar individual e tentar fazer encontrar a formula do semiperímetro dela.

Observe na formula abaixo que para se eu somar o a e subtrair o a novamente a formular da primeira parte multiplicada não se altera, assim como fazer isso na segunda parte com o c e na terceira com o b:

Então, observe que (b + c + a - 2a) vai ser igual a (b + c - a), e que (a + b + c - 2c) será igual a

(a + b - c), assim como, (a + c + b - 2b) será igual a (a - b + c). Apenas reescrevemos a formula de outa forma para encontrar a formula do semiperímetro nela... mas sua essência, seu resultado não altera.

Separando a formula do semiperimetro para chamá-lo de p teremos:

Voltando na fórmula e substituindo temos:

Passando o expoente 2 que esta junto com o A para o outro lado temos a fórmula:

Exemplo de uso:

Calcular a área de um triângulo de lados 3 cm, 4 cm e 5 cm.

p=3+4+52=122=6 cm

A=6(6−3)(6−4)(6−5)−−−−−−−−−−−−−−−−−√

A=6(3)(2)(1)−−−−−−−−√

A=36−−√

Mas, quem foi Heron (Herão)?

Segundo o site https://conhecimentocientifico.r7.com/heron-de-alexandria/

Heron de Alexandria foi um dos grandes nomes envolvidos com o estudo da engenharia e matemática. Ele viveu entre os anos 10 d.C e 70 d.C, no Egito Romano, lugar dominado pelo Império Romano na época. Heron fez contribuições significativas para o campo das ciências exatas e, acima de tudo, na geometria.
Nessa área, sua obra máxima é a Métrica, que ficou perdida no tempo por séculos, sendo encontrada somente em 1896. A obra é um compêndio na forma de três livros, cheio de fórmulas e regras recolhidas de diferentes fontes por Heron. Nela há, por exemplo, áreas e volumes de figuras planas e sólidas referente à antiga Babilônia.
Sabe-se muito pouco sobre sua vida, muitos de seus escritos e desenhos foram perdidos no tempo. No entanto, com base nos remanescentes, acredita-se que ele tenha lecionado no Mouseion de Alexandria, local onde ficava a prestigiada Biblioteca de Alexandria.
Isso porque, boa parte de suas notas escritas são direcionadas a cursos de matemática, mecânica, física e pneumática. Além do campo das exatas, o trabalho de Heron levou as primeiras pesquisas formais em cibernética, área oficializada apenas no século XX.

O trabalho e estudo de Heron de Alexandria estão presentes na matemática até hoje.

Apesar de seu nome ser muito mais lembrado por causa da Métrica, ele também desenvolveu um método de cálculo interativo para encontrar a raiz quadrada de um número com precisão arbitrária. Atualmente, existe uma versão desse cálculo interativo empregado nos computadores.
Na geometria, sua fórmula é constantemente usada para calcular a área de um triângulo usando somente as medidas laterais, conhecida como Fórmula de Heron. No Livro I da Métrica, Heron lista meios para descobrir a área de diversas figuras planas e aéreas de superfícies sólidas comuns.
No Livro II o autor apresenta formas de calcular volume de vários objetos sólidos, incluindo cinco sólidos platônicos regulares. Além disso, no Livro III, Heron aborda a divisão de figuras planas e sólidas, de acordo com proporções específicas.
Infelizmente, não são apenas fatos sobre sua vida que o tempo consumiu, mas também muito do seu próprio trabalho. Sobraram poucos estudos referentes à mecânica, por exemplo. Contudo, ficou o suficiente para desencadear mudanças na área.

ÁREA DO TRIÂNGULO EQUILATERO

Triângulos equiláteros são aqueles triângulos que possuem todos os lados com a mesma medida. ou seja, equi = igual, latero = lado.

Observe o triângulo abaixo:

Vamos dividir o triângulo pela reta h de modo a obter 2 triângulos retângulos iguais:

Aplicando pitágoras descobrimos a fórmula para calcular a altura (h) do triângulo:

Agora, aplicando a fórmula da altura na formula padrão de área do triângulo, temos:

Exemplo:

Determine a medida da área de uma região triangular equilátera, com lados medindo 12 metros de comprimento.

A região triangular possui área medindo 36√3 metros.

vídeo demonstrações:

fórmula base da área do triângulo:

Fórmula área do triângulo com circulo inscrito:

Área do triângulo com seno do ângulo:

Área do triângulo com circulo circunscrito

Área do triângulo com semiperímetro

Área do triângulo equilátero

Explicando em vídeo:

Fórmula base de área do triângulo:

Fórmula de área com circulo inscrito.

Fórmula área com seno

Fórmula de área com circulo circunscrito:

Fórmula de Heron - área com perímetro

Fórmula de área para triângulo equilátero

Atividade geogebra: