Triangulos Semelhantes

A semelhança de triângulos consiste, de modo geral, na proporção entre dois ou mais triângulos, ou seja, são proporcionais se, e somente se, todos os seus lados e ângulos internos forem proporcionais ao outro triângulo.

As semelhanças entre os triângulos podem acontecer da seguinte maneira:

Ângulo-Ângulo (AA)

"Se dois triângulos possuem dois ângulos ordenadamente congruentes, então eles são semelhantes." exemplo:

Lê-se: ângulo A é equivalente ao ângulo A' e ângulo B é equivalente ao ângulo B', então:

Triangulo ACB é semelhante ao triangulo A'C'B'.

Lê-se: ângulo A é equivalente ao ângulo D e ângulo C é equivalente ao ângulo E, então:

Triangulo ACB é semelhante ao triangulo FED.

Lembrando que Congruência é: em geometria, duas figuras são congruentes se elas possuem a mesma forma e tamanho.

Logo se dois ângulos possuem a mesma forma e tamanho em um triangulo, os dois triângulos são semelhantes.

Lado-Ângulo-Lado (LAL)

"Se dois lados de um triângulo são proporcionais aos lados homólogos do outro triângulo e se o ângulo entre estes lados for congruente ao correspondente do outro triângulo, então os triângulos são semelhantes." Exemplo:

Lê-se: se a razão entre as linhas b e b´ for igual a razão das linhas c e c´ e, ainda, o ângulo A for equivalente ao ângulo A', o triângulo ABC é semelhante ao triangulo A'B'C'.

Lê-se: se a razão entre as linhas dos pontos AB e DF for igual a razão das linhas dos pontos AC e DE e, ainda, o ângulo A for equivalente ao ângulo D, o triângulo ABC é semelhante ao triangulo DEF.

Então, nesse caso vamos imaginar o seguinte: 

- Temos 2 triângulos onde a 2 linhas que estão na mesma posição são proporcionais, ou seja se eu dividir o comprimento da linha do triangulo 1 com a mesma linha do triangulo 2 o resultado será o mesmo que dividir outra linha do triangulo 1 com a linha correspondente do triangulo 2.

- O ângulo entre essas 2 linhas é igual ao ângulo formado pelas mesmas linhas correspondentes do segundo triângulo.

Se termos essas duas condições os triângulos são semelhantes.

Lado-Lado-Lado (LLL)

"Se dois triângulos possuem os seus lados homólogos proporcionais, então eles são semelhantes." Exemplos:

Lê-se: se a razão entre as linhas a e a', b e b' e c e c' forem iguais, o triângulo ABC é semelhante ao triângulo A'B'C'.

Lê-se: se a razão entre as linhas dos pontos AB e DF, BC e FE e AC e DE forem iguais, o triângulo ABC é semelhante ao triângulo DFE.

Outra situação de semelhança de triangulo é quando os lados são proporcionais, ou seja, a divisão realizada pela linha do triangulo 1 pela linha correspondente do triangulo 2, em qualquer uma das 3 linhas, terão o mesmo resultado.

Exemplo:

Considere os triângulos a seguir. Sabendo que eles são semelhantes, determine os valores de a, b e c. O perímetro do triângulo maior é igual a 84 cm.

Por hipótese, os triângulos são semelhantes. Podemos dizer ainda que a semelhança é pelo caso LLL, ou seja, ABC ~ A’B’C’, portanto:

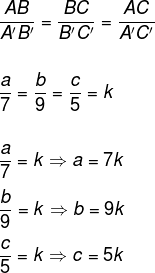
Como o perímetro do triângulo maior é igual a 84 cm, temos que:

a + b + c = 84

7k + 9k + 5k = 84

21k = 84

k =4

Substituindo os valores de k nas igualdades, temos:

a = 7 · (4) → a = 28 cm

b = 9 · (4) → b = 36 cm

c = 5 · (4) → c = 20 cm

História da semelhança dos triângulos:

Cerca de seiscentos anos antes de Cristo, no Egito, foi que se teve a primeira aplicação da Semelhança de Triângulos. A pedido de um mensageiro do faraó, Tales de Mileto - considerado um dos sete sábios da antiguidade clássica – calculou a altura da pirâmide de Quéops. Para desenvolver tal cálculo, Tales fincou uma vara verticalmente no chão e aguardou até o momento em que a sombra e a própria vara tivessem a mesma medida. Quando o esperado ocorreu, Tales disse “Vá, mede depressa a sombra: o seu comprimento é igual à altura da pirâmide”.

Para se obter o valor exato da altura da pirâmide, Tales deveria ainda ter pedido que se somasse metade do lado da base da pirâmide à sombra da mesma, uma vez que, tendo uma base larga, uma parte da sombra da pirâmide não estava ao chão.

Tales imaginou os dois triângulos imaginários demonstrados abaixo para efetuar seu cálculo.

Desse modo:
(retos)

(ângulos de inclinação dos raios solares)

A conclusão que se chega é que os triângulos são semelhantes pelo caso AA.
ΔABC~ΔRST




Então, para achar o valor da altura da pirâmide, fez-se a seguinte proporção: .


Com esse feito matemático, Tales ganhou grande apreciação em sua época e ainda hoje, pelo mesmo motivo somado a outras tantas contribuições, Tales é considerado um dos grandes nomes da matemática.

Vídeo:

Atividade geogebra: