Teorema das Bissetrizes de um triângulo

 A bissetriz é uma semireta que divide o ângulo do triângulo, traçado a partir de sua vértice. Os triângulos possuem ângulos internos e externos, e para cada um desses ângulos, podemos traçar uma bissetriz.

Como encontrar a Bissetriz

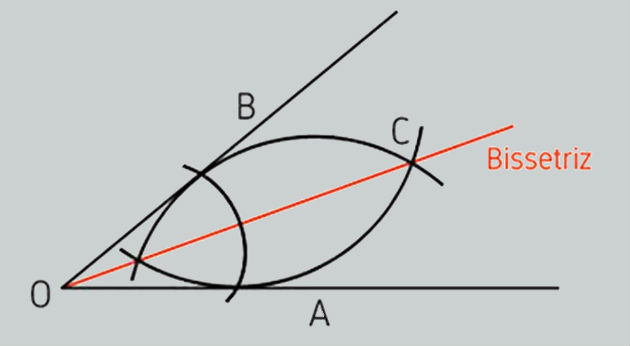
Para encontrar a bissetriz, basta seguir os seguintes passos utilizando o compasso:

- Abra um pouco o compasso e coloque a sua ponta seca no vértice do ângulo.
- Faça um traço de circunferência sobre as semirretas OA e OB.
- Com o compasso aberto, coloque a ponta seca no ponto de intersecção da semirreta OA e faça um traço de circunferência com o compasso virado para dentro do ângulo.
- Faça o mesmo, agora com a ponta seca no ponto de intersecção da semirreta OB.
- Trace uma semirreta do vértice do ângulo até o ponto de intersecção dos traços que acabou de fazer. A semirreta OC é a bissetriz.

Fonte:https://www.todamateria.com.br/bissetriz/ 

Bissetriz interna

As bissetrizes internas são as semiretas traçadas dividindo os ângulos internos do triângulo. A bissetriz traçada a partir de uma vértice, cria na reta oposta ao ângulo uma divisão em 2 segmentos também.

Observe pela figura acima que a bissetriz traçada a partir da vertice A, gera um novo ponto no seguimento BC, chamado de S. Esse ponto divida essa reta nas retas x e y.

Existe uma proporção entre as retas adjacentes aos dois novos seguimentos  gerados com a bissetriz, com isso, podemos escrever essa proporção da seguinte maneira:

As três bissetrizes internas do triângulo são concorrentes, e o ponto de encontro delas é o incentro, que é o centro da circunferência inscrita no triângulo, e este ponto também é equidistante de todos os lados do triângulo.

Exemplo:

Qual é o valor do segmento AC?

Aplicando a relação existente no teorema das bissetrizes internas temos:

Agora basta resolver:

Bissetriz Externa:

Ao prolongar as linhas que formam os triângulos, percebemos os ângulos externos. Assim, saindo de uma das vértices, podemos traçar uma bissetriz.

Quando a bissetriz externa intercepta o prolongamento do lado oposto, formam segmentos proporcionais aos lados adjacentes.

Na figura acima podemos perceber que:

x = a + y

e que a proporcionalidade é dada por:

Exemplo:

qual é o valor de x?

Vamos montar a proporção e resolver:

Duas bissetrizes externas de dois vértices diferentes, junto com a bissetriz interna do terceiro vértice do triângulo também são concorrentes e se encontram no exincentro dele, que é tangente a um lado do triângulo e aos prolongamentos dos outros dois lados deste triângulo.

Vídeo:

atividade geogebra: