Triângulo de Pascal

O triângulo de Pascal (alguns países, nomeadamente na Itália, é conhecido como Triângulo de Tartaglia ou na china como triangulo Yang Hui) é um triângulo numérico infinito formado por números binomiais , onde  representa o número da linha e  representa o número da coluna, iniciando a contagem a partir do zero.

Ele é um triangulo aritmético infinito e bastante antigo na matemática. Essa representação geométrica foi estudada pelo matemático chinês Yang Hui (1238-1298) e por muitos outros matemáticos.  

Onze séculos antes de Pascal, Al-Karkhi conseguiu as primeiras soluções numéricas do triângulo, mas foi Pascal quem descobriu a maioria de suas propriedades e relações, o que justifica o nome que é dado ao triângulo.

Foram muitos os matemáticos que, um século antes de Pascal, trabalharam com o triângulo aritmético. O mais antigo parece ter sido Apianus, matemático alemão. Publicou em 1527 um livro intitulado: Rechnung (Cálculo) cuja capa era o triângulo. No entanto o alemão que mais divulgou o triângulo aritmético foi Stifel, principalmente através da Arithmetica Integra em 1544.

Pouco depois dos alemães, alguns matemáticos italianos redescobriram o triângulo. Tartaglia foi o que mais se dedicou a ele dando-lhe extrema importância em General Tratado di numeri et misure no ano de 1556. Após este matemático, também outros se dedicaram ao tema como Cardan, Bombelli.De entre os franceses o que mais divulgou o triângulo antes de Pascal foi Peletier, através da sua Arithmétique, sendo a sua primeira edição em 1549. Também Girard (1629), Mersenne (1636) e outros conheciam este triângulo.

Mas como construímos o triangulo de pascal?

O triangulo de Pascal é construído através de combinações, colocando os números binomiais de mesmo numerador na mesma linha e os coeficientes de mesmo denominador na mesma coluna. 

Ao calcularmos o número binomial conforme aprendemos no post https://didaticursos.blogspot.com/2021/06/numeros-binomiais-ou-coeficiente.html, vimos que quando p = 0 nossa resposta é 1 e quando n = p também a resposta é 1.

logo:

Agora também vimos que quando p = 1 o valor é n então:

Os demais precisamos calcular:

E assim sucessivamente, ficando:

Mas para agilizar a construção, ao invés de calcular dessa forma, podemos fazer de uma maneira mais rápida, através da relação de Stifel (para conhecer mais acesse: https://didaticursos.blogspot.com/2021/06/relacao-de-stifel.html):

Após a definição de 1  para p=0 e n=p, vamos ir somando o número de cima com o número a esquerda dele:

Após construir a linha 2, é possível construir a linha 3 realizando o mesmo procedimento.

Continuando esse procedimento, encontraremos todos os termos (neste caso, até a linha 5), mas é possível construir quantas linhas forem necessárias.

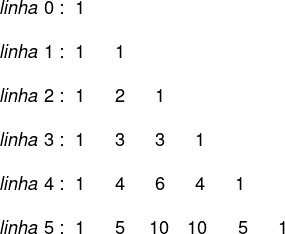
Propriedade do Triângulo de Pascal:

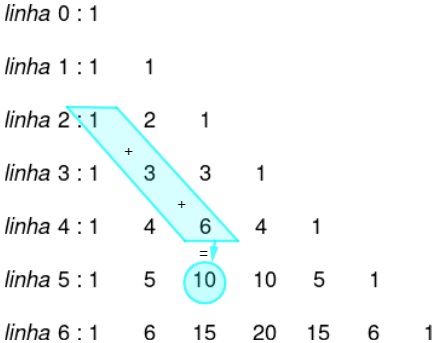
- A primeira propriedade é o que acabamos de ver, que o valor de um numero binomial é a soma do número acima dele com a esquerda desse número de cima.

Essa propriedade é conhecida como relação de Stifel e é importante por facilitar a construção do triângulo e encontrarmos os valores de cada uma das linhas.

- A soma de todos os termos de uma linha é calculada por:

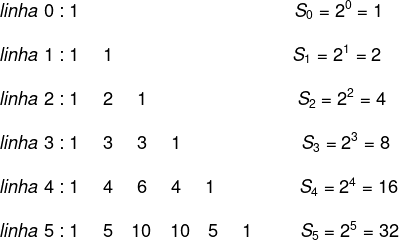
Sn=2n, em que n é o número da linha.

Exemplos:

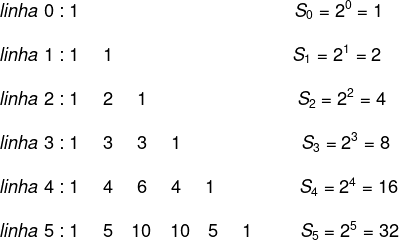
Com essa propriedade, é possível saber a soma de todos os termos de uma linha sem precisar necessariamente construir o triângulo de Pascal. A soma da linha 10, por exemplo, pode ser calculada por 210 = 1024. Ainda que não se conheçam todos os termos, já é possível saber o valor da soma de toda a linha.

-  A soma dos termos que sequencia desde o começo uma determinada coluna p até uma determinada linha n é igual ao termo que está na linha n+1 posterior e coluna p+1 posterior, como é mostrado a seguir:

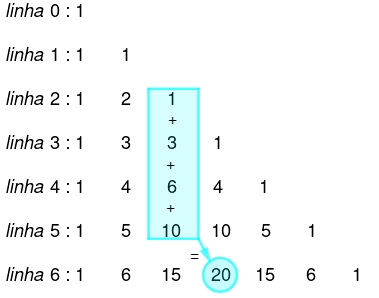
- A soma de uma diagonal que começa na coluna 0 e vai até o termo que se encontra na coluna p e linha n é igual ao termo que está na mesma coluna (p), mas na linha abaixo (n+1), como mostrado na imagem:

- Existe uma simetria nas linhas do triângulo de Pascal. O primeiro e o segundo termo são iguais, o segundo e o penúltimo são iguais e assim sucessivamente.

Para que usamos triangulo de pascal?

Devido à forma como os números estão dispostos é possível encontrar várias propriedades entre eles. Essas propriedades são úteis em alguns cálculos matemáticos, sendo usadas na antiguidade para o cálculo de raizes quadradas ou cúbicas, ou mais recentemente, no cálculo das probabilidades. Os termos do Binómio de Newton, podem ser encontrados a partir dos números presentes no triângulo, assim como, os termos que formam a Sequência de Fibonacci. Podem também ser encontrados nas suas diagonais, os números triangulares ou os números quadrados. Vários padrões foram recentemente descobertos, como por exemplo o desenho do Triângulo de Sierpinski.

Um grande uso para ele está em encontrar os valores dos Binômios de Newton (para ver mais acesse: https://didaticursos.blogspot.com/2021/06/binomio-de-newton.html), pois para calcular valores de binômios acima de potência de 3 - exemplo: (a + b)⁵ - é muito mais difícil e trabalhoso fazer pela propriedade distributiva.

Vídeo:

atividade geogebra: