Teorema Linear de Tales
O Teorema Linear diz o seguinte: "A intersecção de um feixe de retas paralelas por duas retas transversais forma segmentos proporcionais."
Para entender melhor, vamos analisar a figura acima, note que as retas r, s e t são paralelas uma a outra, ou seja, estão na mesma direção. já as retas a e b são transversais (corta) as retas r, s e t, e não são paralelas uma a outra pois não estão indo na mesma direção.o símbolo de paralelismo é representado da seguinte maneira: // então no caso da nossa figura podemos dizer que r//s//t.
Segundo o teorema de Tales existe uma relação entre os pontos formados pela intersecção A, B, C, A', B', C':
Analisando isso ,podemos reescrever essa proporcionalidade da seguinte maneira:
Como usar?
Temos a seguinte figura:
Agora o próximo passo é a multiplicação cruzada, nisso é possível observar que é indiferente a proporção, pois para ambos a expressão gerada será a mesma:
Mas onde vou aplicar esse Teorema?
Tem uma questão do Enem que pode exemplificar o uso:
(Enem) A planta de determinado bairro de uma cidade apresentou o desenho a seguir. O responsável pelo departamento de obras do município constatou a ausência de algumas medidas nessa planta, as quais ele representou no projeto por x e y.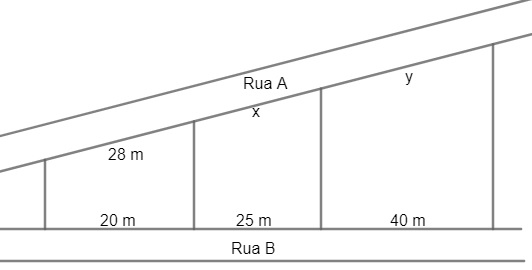
Com base nos dados do projeto, esse responsável pôde calcular corretamente os respectivos valores de x e y:
a) 35 m e 56 m
b) 25 m e 40 m
c) 35 m e 70 m
d) 56 m e 70 m
e) 56 m e 84 m
Aqui podemos aplicar o Teorema de Tales.
Vamos começar calculando o X:
Logo X tem 35metros.
Para calcular Y, podemos usar a proporção tanto de 28/20 = Y/40 quanto 35 (valor encontrado de x)/25 = Y/40.
y = 56 metros.
Logo a resposta correta é A.
História do Teorema de Tales
O teorema foi desenvolvido pelo filósofo, astrônomo e matemático grego Tales de Mileto (624 a.C.- 558 a.C.) e, por isso, recebe esse nome.O experimento de Tales foi realizado através da observação de uma sombra da pirâmide. A partir disso, ele conseguiu calcular a altura da pirâmide Quéops, no Egito, com base na sombra que ela projetava.
Considerado o “Pai da Geometria Descritiva”, Tales contribuiu para o avanço dos estudos de razão e proporção, que até os dias de hoje são utilizados para calcular distâncias.
vídeo:
Atividade geogebra:











