Resolvendo raízes não exatas

Existem algumas formas de resolver raízes não exatas, vamos conhecer cada uma delas?

Para conhecer mais sobre raízes de números naturais exatas, acesse: https://didaticursos.blogspot.com/2020/10/raiz-de-numeros-naturais.html

METODO 1: Sucessões de tentativas.

Vamos pensar na raiz de 5:

√5

se pensarmos em potencias possíveis próximas teremos

2² = 2x2 = 4

3² = 3x3 = 9

logo a resposta de √5 esta entre 2 e 3 uma vez que √4 < √5 < √9.

Nesse caso, vamos por tentativa entre 2 e 3, exemplo:

2,5² = 2,5 x 2,5 = 6,25

logo o valor é menor que 2,5

2,4² = 2,4 x 2,4 = 5,76

2,3² = 2,3 x 2,3 = 5,29

2,2² = 2,2 x 2,2 = 4,84

então descobrimos que o resultado esta entre 2,2 e 2,3. vamos testar 2,25?

2,25² = 2,25 x 2,25 = 5,06

2,24² = 2,24 x 2,24 = 5,01

2,23² = 2,23 x 2,23 = 4,97

Logo a resposta aproximada com 2 casas para √5 será 2,23 - pegamos o menor valor aproximado, uma vez que não deu exata, porém caso sinta necessidade pode continuar tentando adicionando uma terceira casa no 2,23.

na calculadora teremos como resposta: 2,2360679774997896964091736687313

METODO 2: Método Babilônico.

Para fazer esse método temos que realizar os seguintes passos:

Inicie com um número positivo arbitrário r (preferencialmente menor e próximo da raiz );
Substitua r pela média de r e $\scriptstyle \frac{n}{r};$
Repita o segundo passo para obter uma aproximação melhor.

Lembrando que esse método é de aproximação, tendo uma pequena margem de erro.

Vamos ao exemplo:

√55

1 - Inicie com um número positivo arbitrário r.

Ache o menor quadrado perfeito que mais se aproxima do número dado. Nesse caso o quadrado que mais se aproxima é 49 (7x7).

Nota: Usa-se sempre o quadrado menor que o número procurado, mesmo que o quadrado maior seja mais próximo.

Extraia a raiz quadrada do quadrado que mais se aproximou. A raiz quadrada de 49 é 7. Nesse exemplo chamaremos 7 como A (A = 7).

2 - Substitua r pela média de r e n/r

Divida o número original por A, ou seja, 55 / 7 = 7,85. Nesse exemplo chamaremos 7,85 como B (B = 7,85).
Somamos A com B e dividimos por 2.
7 + 7,85 = 14,85
14,85 / 2 = 7,425
O resultado chamaremos de C (C = 7,425).

3 - repita o segundo passo para obter uma aproximação melhor
Agora dividimos o número original (nesse caso 55) por C.
55 / 7,425 = 7,407
O resultado chamaremos de D (D = 7,407).
Novamente, usando do mesmo procedimento, somaremos C e D e dividimos por 2.
7,425 + 7,407 = 14,832
14,832 / 2 = 7,416
Esse número chamaremos de E (E = 7,416).

E assim podemos continuar repetindo. Mas pararemos aqui com a resposta de que √55 = 7,416

Na calculadora a √55 7,4161984870956629487113974408007

METODO 3 - Equação de Pell e Aritmética Mental

A equação de Pell permite encontrar a parte inteira de uma raiz quadrada simplesmente subtraindo inteiros ímpares até não ser possível a subtração.

Vamos tentar aplicar a equação de Pell em uma raíz exata:

√121

121 - 1 = 120

120 - 3 = 117

117 - 5 = 112

112 - 7 = 105

105 - 9 = 96

96 - 11 = 85

85 - 13 = 72

72 - 15 = 57

57 - 17 = 40

40 - 19 = 21

21 - 21 = 0

fizemos a conta em 11 passos e chegamos a zero, logo nossa raíz é exata e dará 11.

ou seja 11 x 11 = 121

√16

16 - 1 = 15

15 - 3 = 12

12 - 5 = 7

7 - 7 = 0

Zerou confirmando que a raíz é exata e fizemos em 4 passos, logo a raiz de 16 é 4 pois 4 x 4 = 16

Vamos tentar agora uma raíz não exata, por exemplo √19

para calcular a parte inteira da raiz quadrada de 19, calcula-se a sequência:

19 – 1 = 18

18 – 3 = 15

15 – 5 = 10

10 – 7 = 3

3 - 9 = Acabou por aqui

Como 3 é menor que 9 que seria o próximo impar a ser diminuído, logo paramos por aqui, e como fizemos em 4 passos, logo nossa parte inteira é 4.

Agora para achar as casas decimais fazemos o seguinte:

resultado do último passo * 100 e número de passos da sequência anterior * 20 + 1

então teremos aqui:

3 x 100 = 300

4 x 20 + 1 = 81

então continuaremos assim:

300 - 81 = 219

219 - 83 = 136

136 - 85 = 51

51 - 87 = não da, parou por aqui.

Logo fizemos em 3 passos, então o primeiro digito depois da virgula é 3, ficando 4,3

Se quisermos saber mais casas, repetimos os passos anteriores:

resultado do último passo * 100 e número de passos da primeira sequencia como dezena e da sequencia sequência anterior como unidade * 20 + 1

51 * 100 = 5100

primeira sequencia = 4 como dezena = 40

sequencia anterior =3

logo usaremos 43

43 * 20 + 1 = 861

continuando então:

5100 - 861 = 4239

4239 - 863 = 3376

3376 - 865 = 2511

2511 - 867 = 1644

1644 - 869 = 775

775 - 871 = Não da, logo parou por aqui.

Aqui fazemos em 5 passos logo o segundo número depois da virgula é 5, ficando então 4,35

Na calculadora temos como resposta: 4,3588989435

Mais um exemplo:

√7

7 - 1 = 6

6 - 3 = 3

3 - 5 = Não da, logo parou aqui

foram 2 passos logo o valor inteiro é 2.

agora pegamos o ultimo resultado * 100 e o número de passos * 20 + 1

logo:

3 x 100 = 300

2 * 20 + 1 = 41

300 - 41 = 259

259 - 43 = 216

216 - 45 = 171

171 - 47 = 124

124 - 49 = 75

75 - 51 = 24

24 - 53 = Não da, parou por aqui

Foram 6 passos, logo a primeira casa depois da virgula é 6. ficando 2,6.

para continuarmos faremos de novo o ultimo resultado * 100 e o primeiro numero de passos como dezena e o ultimo como unidade * 20 + 1

24 * 100 = 2400

26 * 20 + 1 = 521

2400 - 521 = 1879

1879 - 523 = 1356

1356 - 525 = 831

831 - 527 = 304

304 - 529 = Não da, parou por aqui

foram 4 passos, logo o próximo número é 4 ficando: 2,64

Na calculadora temos: 2,6457513111

MÉTODO 4 - Aproximação por quadrado da soma de dois termos

Sejam p e q pertencentes aos racionais estritamente positivos e p é o quadrado perfeito mais próximo de q:

$p\cong q$
$p-q\cong 0$
$(p-q)^2\cong 0$
$p^2-2pq+q^2\cong 0$
$p^2+2pq+q^2\cong 4pq$
$(p+q)^2\cong 4pq$
$(p+q)\cong \sqrt{4pq}\cong 2\sqrt{p}\sqrt{q}$
$\sqrt{q}\cong \frac{p+q}{2\sqrt{p}}$

Deduzimos, desse modo, a fórmula para o cálculo de uma raiz quadrada de qualquer número racional:

$\sqrt{q}\cong \frac{p+q}{2\sqrt{p}}$

Vejamos alguns exemplos:

√32

o quadrado perfeito ao redor é √25 = 5 x 5 e √36 = 6 x 6... Como 36 é mais próximo de 32 usaremos ele, usando a formula teremos

p = 36

q = 32

√65 =

Nesse caso as duas raízes perfeitas são √64 = 8 e √81 = 9

Logo usaremos o √64 pois é mais perto, então:

p = 64

q = 65

MÉTODO 5 - Método de Herão.

Herão de Alexandria foi um matemático de destaque com muita controvérsia sobre a época em que viveu, havendo estimativas que variam de 150 a.C. a 250 d.C.. seus trabalhos de Matemática e Física são numerosos e variados, sendo considerado um enciclopedista. Em seu Livro A Métrica, encontra-se o método de Herão de aproximar a raiz quadrada de um número inteiro não-quadrado perfeito. Tal método é hoje utilizado com freqüência por computadores e permite sucessivas aproximações.

Dada a raiz quadrada de um número n, assumindo a0 como uma aproximação inicial, temos:

Uma melhor aproximação será dada pela próxima iteração:

Assim prossegue e a cada iteração melhora a aproximação da raiz.

A saber: Se n = a ∙ b, então (a + b)/2 é uma aproximação de √n, que melhora com a proximidade de a e b.

Após a escolha da aproximação inicial a0, podemos construir o algoritmo:

Onde, para cada iteração k, para todo k = 1, 2, 3, …, encontramos uma raiz ak mais aproximada de n.

Surge então a questão: Até quando essas iterações seguem-se? Para evitar que o programa entre numa rotina de cálculos infinitos, inicialmente devemos impor limites, não para as iterações, mas para o erro da aproximação. Ou seja, se quisermos obter uma aproximação de uma raiz com pelo menos 5 casas decimais corretas, com o erro E < 10^{– 5} , por exemplo, devemos impor uma precisão ε = 1 . 10^{– 5} e devemos, a cada iteração, fazer o teste da raiz aproximada para checar se satisfaz a precisão ε imposta inicialmente. O erro é dado por E = |(a_k)² – n|. Se o valor absoluto do quadrado da raiz aproximadaa_k, subtraída de n for menor que a precisão ε, então tome a_kcomo raiz aproximada.

Exemplo: Aproximar √3 pelo método de Herão com precisão de ε = 1 . 10^{– 4}.

Como a raiz quadrada de 3 está entre 1 e 2, tomamos como aproximação inicial a₀ = 1,5.

Testamos o erro da aproximação inicial a₀. Como |1,5² – 3| > 10^{– 4}, continuamos as iterações:

Fazemos:

k = 1

Como |1,75² – 3| > 10^{– 4}, continuamos as iterações:

k = 2

Como |1,732142857² – 3| > 10^-4, continuamos as iterações:

k = 3

Como |1,732058100147² – 3| < 10^-4, tomamos a₃ como raiz aproximada de √3, com precisão até a sétima casa decimal.

Na calculadora o resultado de √3 é 1,7320508076

MÉTODO 6 - Aproximação de derivada.

Para o cálculo da raiz aproximada de um determinado número y, escrevemos y como $y=x\pm \Delta x$ e utilizaremos a fórmula:

$\sqrt{x\pm \Delta x}\cong \sqrt{x}\pm \frac{\Delta x}{2\sqrt{x}}$

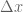
Onde: $x$ é o número mais próximo de y que é quadrado perfeito (maior ou menor que x) e $\Delta x$ é a diferença entre x e y ou entre y e x.

Exemplo: Vamos calcular a raiz quadrada de 7, ou seja, $\sqrt{7}$ .

O número quadrado perfeito mais próximo de 7 é 9, assim escrevemos: 7=9-2. Assim, temos $x=9$ e $\Delta x=2$ . Logo,

$\sqrt{9-2}\cong \sqrt{9}-\frac{2}{2\sqrt{9}}=3-\frac{2}{6}=2,66$ .

Na calculadora √7 = 2,6457513111

Outro exemplo: √5

√4 = 2

√9 = 3

√4 é o mais próximo.

logo:

Na calculadora √5 = 2,236067975

vídeo:

Pesquisar este blog

Descomplicando a matemática