Polígonos - o que é, classificação e cálculos
Em geometria, um polígono é uma figura fechada com lados. A palavra "polígono" vem da palavra em grego "polígonos" que significa ter muitos lados ou ângulos.
Os polígonos podem ser simples ou complexos. Os polígonos simples são aqueles cujos segmentos consecutivos que o formam não são colineares, não se cruzam e se tocam apenas nas extremidades conforme figura acima.
Quando existe intersecção entre dois lados não consecutivos, o polígono é chamado de complexo conforme figura abaixo:
Cada polígono tem um nome de acordo com a quantidade de lado.
Observe que com exceção ao triangulo e ao quadrado as palavras são formadas pela quantidade de lados + gono.
A junção das retas que formam os lados de um polígono com o seu interior é chamada de região poligonal. Essa região pode ser convexa ou côncava.
Os polígonos simples são chamados de convexos quando qualquer reta que une dois pontos, pertencente a região poligonal, ficará totalmente inserida nesta região. Já nos polígonos côncavos isso não acontece.
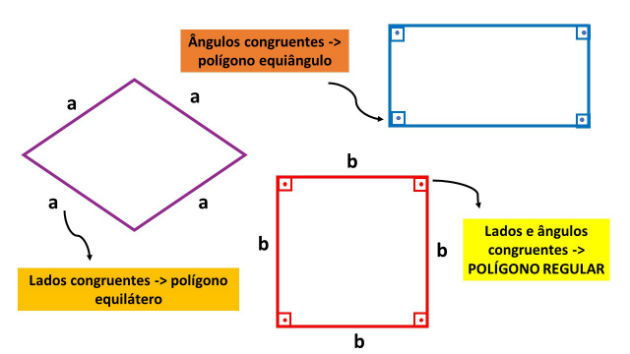
Quando um polígono apresenta todos os lados congruentes entre si, ou seja, possuem a mesma medida, ele é chamado de equilátero. Quando todos os ângulos têm mesma medida, ele é chamado de equiângulo.
Os polígonos convexos são regulares quando apresentam os lados e os ângulos congruentes, ou seja, são ao mesmo tempo equiláteros e equiângulos. Por exemplo, o quadrado é um polígono regular.
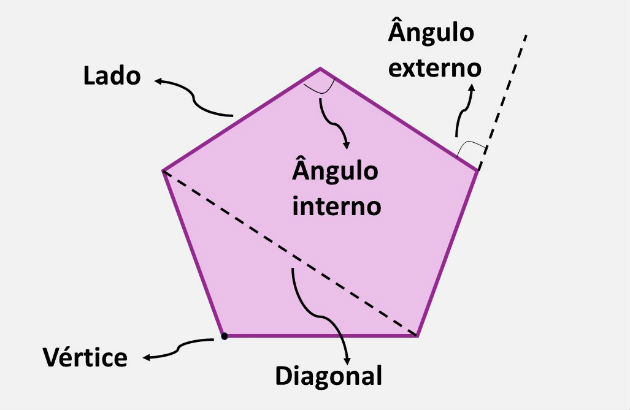
Elementos de um Polígono
Vértice: corresponde ao ponto de encontro dos segmentos que formam o polígono.
Lado: corresponde a cada segmentos de reta que une vértices consecutivos.
Ângulos: os ângulos internos correspondem aos ângulos formados por dois lados consecutivos. Por outro lado, os ângulos externos são os ângulos formados por um lado e pelo prolongamento do lado sucessivo a ele.
Diagonal: corresponde ao segmento de reta que liga dois vértices não consecutivos, ou seja, um segmento de reta que passa pelo interior da figura.
CÁLCULOS COM POLIGONOS:
NÚMEROS DE DIAGONAIS:
É possível calcular o número de diagonais do polígono, através da formula:
onde:
d = número de diagonais.
n = número de lado do polígono.
Exemplo:
Determine o número de diagonais de um polígono com:
a) 8 lados (octógono).jpg)
O octógono possui 20 diagonais.
b) 12 lados (dodecágono)
.jpg)
Mas de onde vem essa formula?
Observe a figura abaixo:
Seja
Mas se escolhendo um vértice como extremidade temos
Como ao fazer a diagonal, por exemplo, das linhas A1 e A4 é igual a fazer a diagonal da linha A4 e A1, ou seja a ordem dos elementos não importam pois gerarão o mesmo resultado, temos que assim como fazemos com a combinação (https://didaticursos.blogspot.com/2021/05/combinacao.html) descontar essas repetições, como no caso são 2 teremos o fatorial de 2 (2!).
logo:
n(n-3)/2!
como 2! = 2 . 1 que é igual a 2. Temos a formula apresentada:
SOMA DOS ÂNGULOS INTERNOS:
A soma dos ângulos externos dos polígonos convexos é sempre igual a 360º. Entretanto, para obter a soma dos ângulos internos de um polígono é necessário aplicar a seguinte fórmula:
Sendo:
S = Soma dos ângulos internos.
n = número de lados.do polígono.
Para calcular o valor de cada ângulo interno, basta pegar o valor da soma dos ângulos internos e dividir pelo número de lados, ou seja:
onde:
ai = angulo interno
n = número de lados
Exemplo:
Qual é o valor da soma dos ângulos internos de um icoságono convexo?O icoságono convexo é um polígono que apresenta 20 lados, ou seja n = 20. Aplicando esse valor na fórmula, temos:
Assim, a soma dos ângulos internos do icoságono é igual a 3240º.
e cada ângulo interno mede:
ai =si/n
ai = 3240/20
ai = 162º
Mas de onde vem a fórmula?
Vamos observar as figuras abaixo:
Em um triângulo a soma dos ângulos internos é 180º. logo:
a + b +c = 180º
Já em um quadrado, se escolhermos um vértice e traçarmos a diagonal temos 2 triângulos.
Logo teremos: 2 . 180º = 360º
observe que o quadrado tem 4 lados e junto ao 180º foi multiplicado por 2. E ainda, que 4 - 2 = 2
Já em um pentágono, se pegarmos uma vértice e criarmos as diagonais, teremos 3 triângulos.
Logo: 3 . 180º = 540º.
observe que o pentágono tem 5 lados e que junto aos 180º foi multiplicado por 3. E ainda que: 5 - 2 = 3.
Se fizermos isso nos demais polígonos, será possível observar o mesmo padrão, o numero de lados do polígono subtraído de 2 e depois multiplicado por 180ºnos dará a soma do ângulo interno. Por isso a fórmula:
SOMA DOS ÂNGULOS EXTERNOS:
A soma dos ângulos externos de um polígono é sempre igual a 360°.
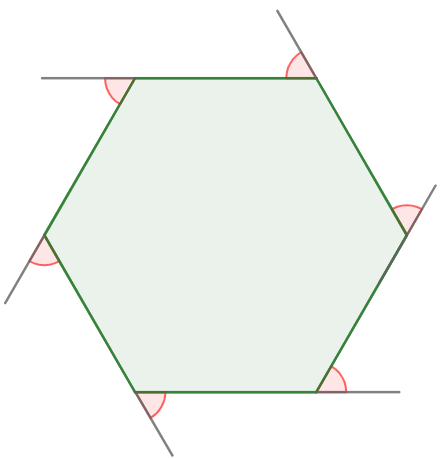
Se= 360º
onde :
Se = ângulo externo.
Se quisermos descobrir o ângulo externo de cada um dos ângulos, basta dividir 360 pelo número de lados do polígono.
ae = 360/n
onde:
ae = ângulo individual
n = número de lados.
Área e perímetro dos Polígonos:
O perímetro de um polígono nada mais é do que a soma de todos os lados.exemplo:
1,3 + 2 + 1,3 + 1,3 + 2 + 1,3
9,2 cm
Já para calcular a área de um polígono, basta encontrarmos figuras conhecidas de área como quadrados e triângulos, onde a fórmula para calculo de área de um quadrado ou retângulo é:
Squadrado = base x altura
e como o triangulo é a metade de um quadrado como visto anteriormente, a fórmula de área de um triangulo é:
Striangulo = (base x altura)/2
Exemplo:
calcule a área do hexágono abaixo:
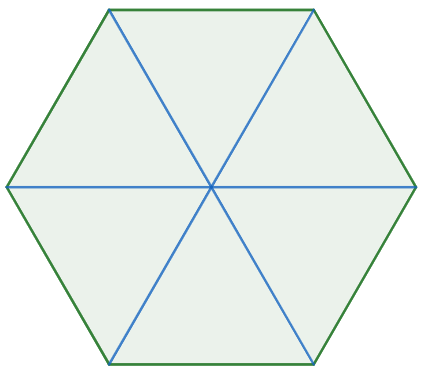
Inicialmente, considere um hexágono regular e todos os segmentos de retas que liguem o centro do polígono a cada vértice. Assim:
Perceba que, devido ao fato do hexágono ser regular, ao dividi-lo, encontramos seis triângulos equiláteros, logo, a área do hexágono é seis vezes a área do triângulo equilátero, ou seja:
Perceba que, devido ao fato do hexágono ser regular, ao dividi-lo, encontramos seis triângulos equiláteros, logo, a área do hexágono é seis vezes a área do triângulo equilátero, ou seja:
calculo de diagonais dos polígonos:
vídeo dos ângulos internos:
vídeo de perímetro e área do polígono
Atividade geogebra:
