Números Binomiais ou coeficiente binomial
Expressão binomial são dois elementos incógnitos ligados por soma ou subtração, por exemplo:
(x + y)
(2y - x)
- (n+p)0= 1
- (n+p)1= (n+p)
- (n+p)2= n² + 2np + p²
- (n+p)3= n³ + 3n²p + 3np³ + p³
Lembram: quadrado do primeiro mais 2 vezes o primeiro vezes o segundo mais o quadrado do segundo? https://didaticursos.blogspot.com/2020/10/produtos-notaveis.html
Porém nesse caso, aprendemos a solucionar binômios com expoentes menor ou igual a 3, e agora estudaremos, através dos binômios de Newton, com expoente maior que 3.
Os Coeficientes ou Números Binomiais são formas algébricas de representar um valor. Ele é genericamente expressado por “n” sobre “p”, dentro de um parênteses, podemos entender mais sobre o uso de "n" e "p" em triângulo de Pascal (para conhecer acesse: https://didaticursos.blogspot.com/2021/06/triangulo-de-pascal.html) onde n se refere a linha e p a coluna. Esse valor pode ser calculado desenvolvendo-se uma fórmula com fatorial, semelhante a da análise combinatória. os números binomiais são uma ferramenta que acelerou os avanços na matemática e na engenharia, porque facilitaram o cálculo de produtos notáveis
Propriedade dos números binomiais:
Binômios particulares: Existem 3 casos que obtemos o resultado do número binomial sem precisar fazer o desenvolvimento do calculo;
- Quando n = p o resultado é sempre 1, pois:
testando:
- Quando p = 0, o resultado é sempre 1, pois:
testando:
testando:
Binomiais complementares:
Dois coeficientes binomiais serão do tipo complementares se seus numeradores forem iguais e a soma de seus denominadores for igual ao numerador. E se os binômios são complementares, seus resultados são o mesmo.Exemplo:
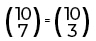
Observe que ambos tem o mesmo numerador 10 (número de cima), e seus denominadores se somarmos 7 + 3 = 10, ou seja, se somarmos os dois denominadores será igual ao numerador, logo, são binomiais complementares.
aplicando a formula:
Confirmando mais uma propriedade.
Historia do Números Binomiais:
Antigamente os números binomiais eram conhecidos como Teorema Binomial, tendo como principais nomes Euclides (c. 330 a. C. - 260 a. C.) com a descrição de produtos notáveis e Newton (1643-1727) no qual avançou o estudo sobre o assunto, desenvolvendo o teorema binomial com expoentes racionais conseguindo excelentes resultados no estudo das
séries infinitas, donde partiu para o tão aclamado cálculo infinitesimal.
Mais tarde, em meados do século XIII, apareceu uma coleção de livros importantes na
China durante a dinastia Tang, dentre eles fazemos menção a Yang Hui. A ele deve-se a mais
antiga apresentação preservada do
―Triângulo Aritmético de Pascal‖. Um
outro chinês, Chu Shi-Kié, em 1303 faz
uma abordagem do mesmo triângulo
aritmético em seu livro. O interessante
deste autor é que ele cita o triângulo
como algo já antigo em seu tempo,
portanto é possível então que o
Teorema Binomial já fosse conhecido
na China de longa data.
No século XV encontra-se a menção a um matemático da corte de Ulugh-Beg, cujo
nome era Al Kashi, o qual teve papel importante nos cálculos de aproximações para 𝞹 Foi ele
o primeiro autor árabe que se tem notícia de lidar com o Teorema Binomial utilizando-o na
forma de Triângulo de Pascal.
Em 1653, com publicação em 1665, Pascal construía seu Triângulo Aritmético, um artifício incrível onde os números ao longo de uma mesma linha
ou diagonal eram os coeficientes sucessivos de uma expansão binomial de (a + b)ⁿ.
vídeo:
atividade no geogebra:














