Binomio de Newton
Binômio de Newton é qualquer binômio (operações de adição ou subtração de 2 incógnitas) com um expoente qualquer. E o nome foi dado em homenagem a Isaac Newton graças aos seus estudos sobre as potências de binômios.
Para calcular os binômios até o expoente 3 utilizamos os produtos notáveis: https://didaticursos.blogspot.com/2020/10/produtos-notaveis.html#more , agora para calcular com expoentes acima de 3 esse processo se torna muito trabalhoso e ocupa muito tempo para tal.
Através dos produtos notáveis, sabe-se que:
(a+b)¹ = a + b
(a+b)² = a² + 2ab + b².
(a + b)³ = a³ + 3a²b + 3ab²+ b³
(a + b)⁰ = 1
ou
observe:
Note que, para cada termo, o expoente de “a” foi diminuindo, começando em n, depois foi para n – 1, e assim sucessivamente até ser 1 no penúltimo termo e 0 no último termo (o que faz com que a letra “a” nem apareça no último termo).
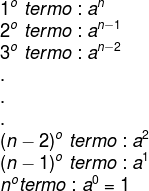
Observe, também que os expoentes de “b” vão sempre aumentando, começando com 0 no primeiro termo (o que faz a letra b nem aparecer no primeiro termo), 1 no segundo termo, e assim sucessivamente até ser igual a n no último termo.

Já os coeficientes são todas as combinações de n elementos tomados de 0 em 0, 1 em 1, 2 em 2, e assim sucessivamente até o último termo, que é a combinação de n elementos tomados de n em n.
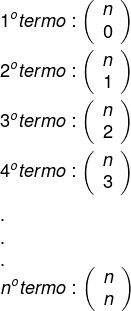
Uma outra ferramenta que nos ajuda a saber o valor de binômios com expoente maior que 3 é o triangulo de Pascal, pois ele já nos da o valor do coeficiente, sem precisar ficar desenvolvendo a conta, apenas aplicando a relação de Stifel.
Para aprender mais sobre triângulo de Pascal acesse:
Propriedade:
1 - O desenvolvimento de (a + b)ⁿ tem n + 1 termos.
Exemplo:
(a+b)¹ = a + b
n = 1número de termos = n+1 = 2
(a+b)² = a² + 2ab + b².
número de termos = n + 1 = 3
(a + b)³ = a³ + 3a²b + 3ab²+ b³
número de termos = n + 1 = 4
2 - Termos equidistantes dos extremos tem coeficiente binomial com mesmo valor absoluto.
Podemos observar isso no proprio triângulo de Pascal onde os valores são simétricos, ou seja, primeiro e ultimo termo é de mesmo valor, o segundo e o penúltimo possuem o mesmo valor e assim por diante.
Soma dos coeficientes:
A soma dos coeficientes do desenvolvimento é obtida substituindo-se as variáveis do binômio pelo número 1.
Exemplo 1:
(4x - y)² = (4 . 1 - 1) = 3² = 9
conferindo:
(4x - y)² = 4²x² - 2 . 4x . y + y² = 16x² - 8xy + y²
logo: 16 - 8 + 1 = 9
Exemplo 2:
(2a + 3b)³ = (2 . 1 + 3 . 1)³ = (2+3)³ = 5³ = 125
conferindo:
(2a + 3b)³ = 2³a³ + 3.2²a².3b + 3.2a.3²b²+ 3³b³
= 8a³ + 3.4a² .3b + 6a.9b² + 27b³
= 8a³ + 36a²b + 54ab² + 27b³
logo: 8 + 36 + 54 + 27 = 125
Atenção:
Se a e b for igual a 1 e a operação for de soma entre os binômios, a soma dos coeficientes poderá, também, ser calculado da mesma forma que somamos a linha do triangulo de Pascal (2ⁿ). conforme aprendido na postagem https://didaticursos.blogspot.com/2021/06/triangulo-de-pascal.html#more
Como por exemplo:
(a + b)³ = a³ + 3a²b + 3ab²+ b³
2ⁿ = 2³ = 8conferindo:
coeficientes: 1 + 3 + 3 + 1 = 8
Termo Geral em função da posição:
O termo geral do binômio de Newton é dado por:
Exemplo:
Qual é o 2º termo do desenvolvimento de (x + 2)³, de acordo com as potências decrescentes de x?
n = 3
Como queremos T2 (2º termo), então:
![]()
Exemplo:
Qual é o 2º termo do desenvolvimento de (x + 2)³, de acordo com as potências decrescentes de x?
n = 3
Como queremos T2 (2º termo), então:
2 = k +1
2 - 1 = k
1 = k
k = 1
Substituindo os valores no temos geral, temos:
conferindo:
Substituindo os valores no temos geral, temos:
(x + 2)³ = x³ + 3x²2 + 3x2²+ 2³
= x³ + 6x² + 12x + 8
Logo o segundo termo é 6x² conferindo com o resultado do calculo.vídeo:
atividade no geogebra:









