Ângulos
Existem algumas classificações para o ângulo de acordo com a sua medida.
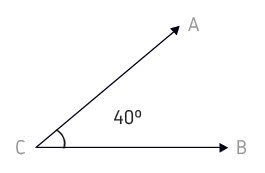
Agudo: É o ângulo que mede menos de 90º
Raso: É o ângulo que mede 180º, ou seja, é uma meia volta, ângulo = 180º.
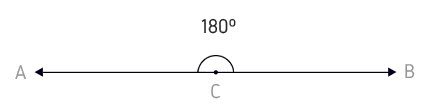
Nulo: É o ângulo que não tem abertura ou seja possui 0º.
Ainda além desses ângulos, temos os ângulos ADJACENTES:
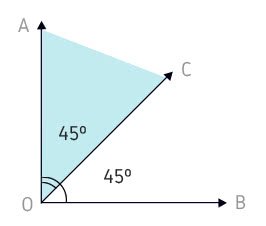
AÔC e AÔB possuem pontos internos em comum. Logo, não são adjacentes.
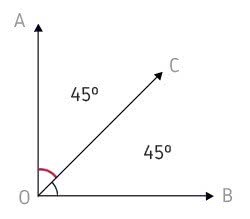
AÔC e CÔB não possuem pontos internos em comum. Logo, são adjacentes complementares.
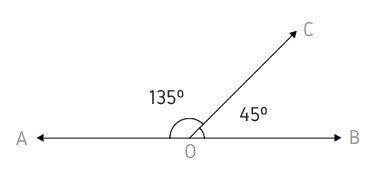
AÔB e AÔC não possuem pontos internos em comum. Logo, são adjacentes suplementares.
Mas afinal de contas, o que é suplementar e complementar que esta escrito acima?Bom, os ângulos adjacentes podem ser classificados como complementares e suplementares:
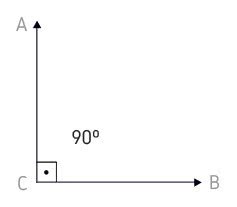
Complementares: A soma dos ângulos adjacentes complementares é 90º. Exemplo:
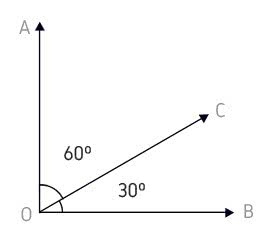
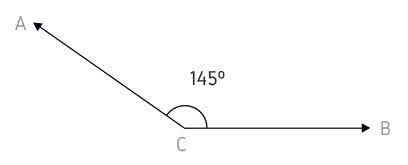
Suplementares: A soma dos ângulos adjacentes suplementares é 180º. Exemplo:
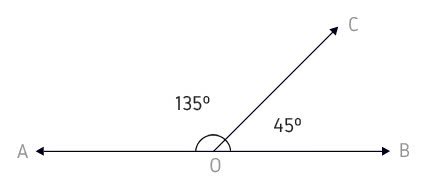
Isso quer dizer que o ângulo de 135º é o suplemento do ângulo que mede 45º.
Ao mesmo tempo, o ângulo de 45º é o suplemento do ângulo que mede 135º.
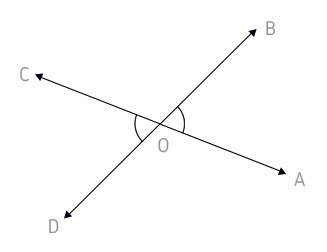
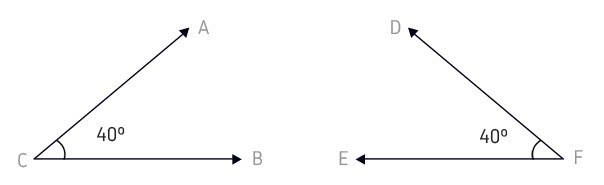
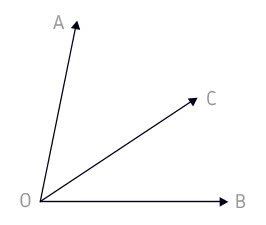
AÔC e CÔB têm em comum o vértice (O) e o lado (OC)
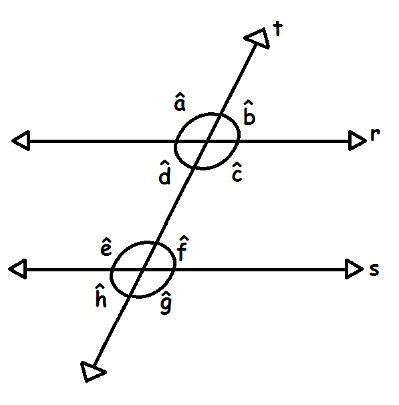
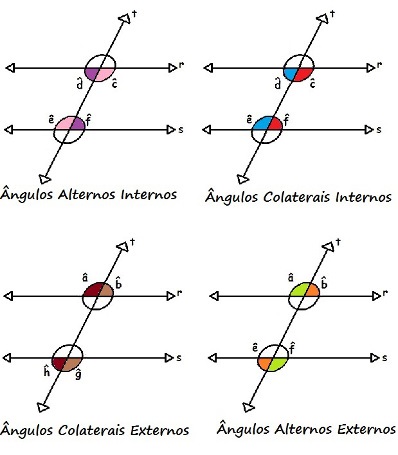
Sabendo que os ângulos formados pelas retas r e t são iguais aos formados pelas retas s e t, podemos afirmar que os pares de ângulos abaixo são correspondentes:
a e e
b e f
c e g
d e h
Estes pares de ângulos colaterais correspondentes, acima mencionados, possuem a mesma medida. Mas sabemos que os ângulos opostos pelo vértice são congruentes, isto é, também possuem a mesma medida. Então, podemos dizer que:
b = d = f = h
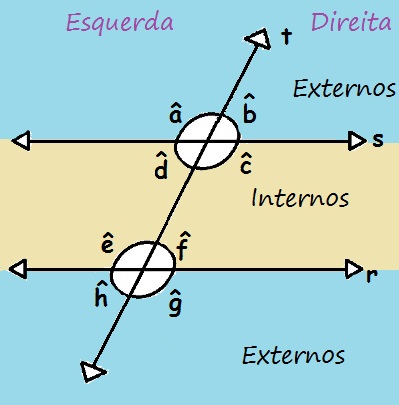
Os ângulos d e f e também e e c podem ser classificados como ângulos alternos internos, pois estão na região interna e em lados alternados. Os ângulos d e e, bem como os c e f, podem ser classificados como ângulos colaterais internos, uma vez que estão na região interna e do mesmo lado em relação à reta t.
Semelhantemente, os ângulos a e h, assim como b e g, são ângulos colaterais externos, pois estão na região externa e do mesmo lado em relação à reta t. Assim como os ângulos a e g, bem como b e h, são ângulos alternos externos, pois estão na região externa e em lados alternados em relação à reta transversal t.
Na figura a seguir, podemos ver claramente os ângulos alternos internos, colaterais internos, alternos externos e colaterais externos formados através de duas retas paralelas cortadas por uma transversal: