Permutação
Tendo em mãos uma sequência ordenada qualquer com um número “n” de elementos distintos, qualquer outra sequência formada pelos mesmos “n” elementos reordenados é chamada de permutação.
Desse modo, podemos dizer que, se A é uma permutação de B, então A e B são constituídos pelos mesmos elementos, mas ordenados de forma diferente.
A permutação é uma técnica de contagem utilizada para determinar quantas maneiras existem para ordenar os elementos de um conjunto finito. Fazer uma permuta é realizar uma troca e, nos problemas de combinatória, significa trocar os elementos de lugar, considerando a ordenação desses.
Exemplo:Calcule o número de permutações das letras da palavra AMOR.
Exemplo:
Exemplo 1:
De quantas maneiras podem se distribuir 5 crianças em uma roda?
Primeiro faremos que nem uma permutação simples.
P5=5.4.3.2.1=120
Veja que para cada permutação simples, são criados 5 casos que representam a mesma configuração em uma permutação circular.
Que são a rotação desse círculo nas 5 posições.
Assim como o caso de permutação com repetição, para retirar esses casos repetidos, dividimos pela quantidade que eles aparecem.
PC5=(5.4.3.2.1)/5=4.3.2.1=24
Generalizando, podemos obter a fórmula de permutação circular:
PCn=(n−1)!
Outra forma de chegar na fórmula de permutação circular, é fixar um elemento para ser o “referencial”. Assim, os elementos ficam em posições relativas à este referencial e o valor da permutação circular é a permutação dos outros elementos (n-1)!.
Exemplo2: Uma família é composta por seis pessoas: o pai, a mãe e quatro filhos. Num restaurante, essa família vai ocupar uma mesa redonda. Em quantas disposições diferentes essas pessoas podem se sentar em torno da mesa?
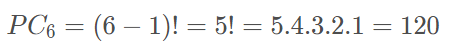
Essas pessoas podem sentar de 120 maneiras diferentes envolta da mesa.
vídeo:
Desse modo, podemos dizer que, se A é uma permutação de B, então A e B são constituídos pelos mesmos elementos, mas ordenados de forma diferente.
A permutação é uma técnica de contagem utilizada para determinar quantas maneiras existem para ordenar os elementos de um conjunto finito. Fazer uma permuta é realizar uma troca e, nos problemas de combinatória, significa trocar os elementos de lugar, considerando a ordenação desses.
Existem 3 tipos de permutação:
- Permutação Simples
- Permutação com repetição
- Permutação circular
Permutação simples:
Permutação simples de n elementos é um arranjo simples de ne elementos tomados n a n. ou seja temos o mesmo número de casas e opções para montar o conjunto.
Sendo Pn as permutações dos n elementos distintos, temos:
Exemplo:
temos então 4 opções e 4 casinhas... logo:
Permutação com repetição:
Se na permutação de n elementos, existirem elementos que apareçam n1 vezes, n2 vezes, ... nr vezes, o número total de permutação com esses elementos repetidos será:
Vamos determinar quantas permutações existem para a palavra OVO.
Observe que mesmo o O não sendo o mesmo na mesma posição, ele forma a mesma palavra. Por isso não podemos utilizar a permutação simples nesse caso, pois é preciso desconsiderar a letra repetida para evitar repetição de palavra. Então:
Temos 3 letras ou seja 3 opções para usar, porém a letra O se repete 2 vezes, logo:
Outro exemplo:
Calcule o número de anagramas da palavra ANTONIA.
Repetindo o 7 é a quantidade de letras na palavra ANTONINA, o 2 é a repetição da letra A que se repete 2 vezes e o outro 2 é a repetição da palavra N que se repete 2 vezes que precisa ser descontado.
Observe que aqui temos as letras A e N que se repetem 2 vezes e não podemos considera-la fazendo a permutação simples, então temos que descontar as repetições de A (2 vezes) e N (2 vezes).
Observe que a palavra Antonina tem 7 letras, ou seja temos 7 opções de letras. Logo:
Permutação Circular:
Quando dispomos de elementos ao redor de um circulo usamos a permutação circular, ou seja, permutação circular é um tipo de permutação composta por um ou mais conjuntos em ordem cíclica. Ocorre quando temos grupos com m elementos distintos formando uma circunferência. A fórmula é dado por:
Exemplo 1:
De quantas maneiras podem se distribuir 5 crianças em uma roda?
Primeiro faremos que nem uma permutação simples.
P5=5.4.3.2.1=120
Veja que para cada permutação simples, são criados 5 casos que representam a mesma configuração em uma permutação circular.
Que são a rotação desse círculo nas 5 posições.
Assim como o caso de permutação com repetição, para retirar esses casos repetidos, dividimos pela quantidade que eles aparecem.
PC5=(5.4.3.2.1)/5=4.3.2.1=24
Generalizando, podemos obter a fórmula de permutação circular:
PCn=(n−1)!
Outra forma de chegar na fórmula de permutação circular, é fixar um elemento para ser o “referencial”. Assim, os elementos ficam em posições relativas à este referencial e o valor da permutação circular é a permutação dos outros elementos (n-1)!.
Exemplo2: Uma família é composta por seis pessoas: o pai, a mãe e quatro filhos. Num restaurante, essa família vai ocupar uma mesa redonda. Em quantas disposições diferentes essas pessoas podem se sentar em torno da mesa?
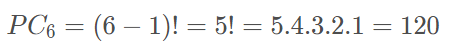
Essas pessoas podem sentar de 120 maneiras diferentes envolta da mesa.
Como saber qual usar, entre arranjo, permutação e combinação????
atividade geogebra:
