Fatorial

 Dado um número natural n, n > 1, chama-se fatorial de n indicado por n!, ao produto de n fatores consecutivos e decrescentes  de n a 1, ou seja:

n! = n . (n-1) . (n-2)..... 3 . 2 . 1, exemplo:

Note que para calcularmos o fatorial, basta multiplicar o número dado, com seu antecessor até chegar a 1.

observação:

0! = 1

1! = 1

História do Fatorial:

O conceito de fatorial (n!) foi organizado pela primeira vez em 1808 por Cristian Kramp (1760-1826), mas a curiosa notação (!) foi cunhada por Francisco de Borja Garção (1759-1829). Aparentemente, a notação foi utilizada involuntariamente em um livro daquele autor para expressar surpresa ou estupefação por um determinado resultado, mas a “notação” foi bem aceita entre os europeus.

Você sabe como surgiu o fatorial? Ele é o resultado da integração por partes de uma sequência numérica utilizada em uma integral especial:



Essa integral recebe o nome de Função Gama (Γ(n)). A função foi batizada por Legendre (1752-1833) em 1811, mas a Função Gama, assim como a Função Beta,  foram encontradas por Euler (1707-1783) em 1729 quando ele pesquisava movimentos harmônicos.

Operações de soma, subtração e multiplicação com fatorial

Quando vamos somar, subtrair ou multiplicar dois fatoriais, é necessário calcular cada um deles separadamente. Não é possível calcular diretamente como uma conta normal. Notem:

a) 2! + 3! = (2 · 1) + (3 · 2 · 1) = 2 + 6 = 8    = > Maneira correta de resolver.

Note que se calcularmos direto não da o  mesmo resultado:

2! + 3! ≠ 5!, onde: 5 . 4 . 3 . 2 . 1 = 120   = > Maneira incorreta de resolver

b) 4! · 2! = (4 · 3 · 2 · 1) · (2 · 1) = 24 · 2 = 48    = > Maneira correta de resolver.

Note que se calcularmos direto não da o  mesmo resultado:

4! · 2! ≠ 12!, onde 12 . 11 . 10 . 9 . 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1 = 479.001.600   => Maneira incorreta de resolver

c) 7! - 5! =(7 · 6· 5· 4 · 3 · 2 · 1) - (5· 4 · 3 · 2 · 1) = 5040 – 120 = 4920   = > Maneira correta de resolver.

Note que se calcularmos direto não da o  mesmo resultado:

7! – 5! ≠ 2!, onde 2 . 1 = 2      => Maneira incorreta de resolver

As seguintes operações não são válidas:
n! + x! = (n+x)!
n! - x! = (n-x)!
n! . x! = (n . x)!

Divisão ou simplificação de fatorial

Para a divisão, também dito simplificação, de um fatorial o processo é um pouco diferente e mais fácil.

Observe:

Então sabendo disso, podemos fazer a fatoração do número maior da divisão até ao número menor da divisão, que o resultado será o mesmo, e calcular o que sobrou dos números fatorados.

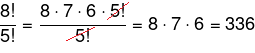
Exemplo 2:

ou seja, seria o mesmo que fazer:

Equação fatorial:

Na matemática, há equações em que os números fatoriais estão presentes, por exemplo:

x – 10 = 4!

x – 10 = 24
x = 24+10
x = 34

Análise Fatorial

A análise fatorial é um método utilizado nos estudos de estatísticas por meio da criação de variáveis. No campo da psicologia ela também é explorada no desenvolvimento de instrumentos psicológicos.

Análise combinatória e Fatorial

Ao realizar o estudo mais aprofundado em análise combinatória, o fatorial de um número sempre aparecerá. Os principais agrupamentos da análise combinatória, que são a permutação, a combinação e o arranjo, usam o fatorial de um número em suas fórmulas. Veremos individualmente cada um um outras postagens.

vídeo:

atividade geogebra: