Propriedade das determinantes

 As propriedades das determinantes podem facilitar muito o calculo dela, através de sua análise das características.

- 1º propriedade - Determinante igual a zero

O determinante de uma matriz quadrada é igual a zero, se a matriz possui:

- Uma fila nula;

- Duas filas paralelas iguais;

- Duas filas paralelas proporcionais;

- Uma fila que é combinação linear as outras filas paralelas.

- Se todos os elementos de uma linha ou de uma coluna da matriz forem multiplicados por um número real p qualquer, então seu determinante também será multiplicado por p.

- Se uma matriz A, quadrada de ordem m, for multiplicada por um número real p qualquer, então seu determinante será multiplicado por pm.

- Se trocarmos de posição duas linhas ou duas colunas de uma matriz, seu determinante será o oposto da matriz anterior.

- O determinante de uma matriz é igual ao determinante de sua transposta:

det A=det At

- Teorema Jacobi: o determinante de uma matriz não se altera quando somamos aos elementos de uma fila uma combinação linear dos elementos correspondentes de filas paralelas.

Exemplo:

Se somarmos os elementos da coluna 1 com o dobro dos elementos da coluna 2, o determinante não irá se alterar.

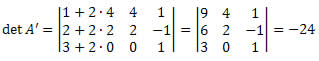
Ver mais na postagem:

https://didaticursos.blogspot.com/2021/04/determinante-teorema-de-jacobi.html

- Matriz triangular: Se os elementos acima ou abaixo da diagonal principal forem iguais a zero, então o determinante da matriz será o produto dos elementos da diagonal principal.

- Teorema de Binet: O determinante do produto de duas matrizes é igual ao produto dos determinantes de cada uma delas. Ver mais sobre o teorema de Binet na postagem: https://didaticursos.blogspot.com/2021/04/determinantes-teorema-de-binet.html

det (A*B) = det A * det B

- Cofator de um elemento: Dada uma matriz A = (aij) m x n chama-se cofator de elemento aij o número:

Em que Dij é o determinante da matriz que se obtém de A eliminando-se a linha i e a coluna j.

ver mais na postagem sobre cofatores: https://didaticursos.blogspot.com/2021/03/cofator-de-uma-matriz.html

- Teorema de Laplace e Cauchy: Numa matriz quadrada a soma dos produtos dos elementos de uma fila qualquer:

* Pelos respectivos cofatores é igual ao determinante da matriz (Teorema de Laplace)

Ver mais na postagem sobre Teorema de Laplace: https://didaticursos.blogspot.com/2021/03/determinante-de-quarta-ordem-ou-mais.html

* Pelos cofatores dos elementos correspondentes de outra fila paralela a zero. (Teorema de Cauchy)

Ver mais na postagem sobre Teorema de Cauchy https://didaticursos.blogspot.com/2021/04/determinante-teorema-de-cauchy.html

-Determinante Vandermonde:

Um determinante é de Vandermonde quando temos:

1º linha ou coluna - só o número 1

2º linha ou coluna - elementos característicos quaisquer

3º linha ou coluna - elementos característicos ao quadrado

4º linha ou coluna - elementos característicos ao cubo

e assim sucessivamente.

O determinante de Vandermonde é igual ao produto de todas as diferenças possíveis entre seus elementos característicos, desde que, o minuendo tenha maior índice que o subtraendo.

Lembrando que na subtração o subtraendo e o minuendo são:

Para entender melhor acesse: https://didaticursos.blogspot.com/2021/04/determinante-vandermonde.html