Determinante - Teorema de Jacobi
Segundo a Teoria de Jacobi - "o determinante de uma matriz não se altera quando somamos aos elementos de uma fila uma combinação linear dos elementos correspondentes de filas paralelas."
Esse teorema reduz o valor dos elementos de uma matriz quadrada (provocando o surgimento de zero), e com esses valores reduzidos fica mais fácil o calculo para encontrar a determinante.
Então o teorema nos mostra que se multiplicarmos um número k em uma fila de uma matriz quadrada, devemos somar o resultado pelos elementos de uma outra fila paralela a ela e o resultado da determinante dessa matriz será igual ao determinante da matriz original.
Vamos ao exemplo para entender melhor:
Vamos aplicar o teorema de Jacobi na seguinte matriz quadrada:
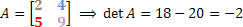
Observe que ao calcular o determinante dessa matriz temos como resultado (-2).
Como a
Vamos multiplicar a primeira linha por (-2) e o resultado vamos somar com a segunda linha. Teremos o matriz:
Observe que o determinante da nova matriz formada é igual a (-2) igual a matriz original. confirmando assim o Teorema de Jacobi.
E se no lugar do (-2) multiplicarmos por (-1):
O determinante ainda continuaria como resultado (-2). Só para escolher o número é bom observar usar um número que multiplicado reduza ao máximo os valores dos elementos da matriz.
Vamos a outro exemplo:
Vamos aplicar agora o Teorema de Jacobi.
Multiplicando os elementos da primeira coluna por (-3) e somando com os elementos da segunda coluna.
Observe que a nova matriz também terá o determinante 117, assim como a matriz original.
Outro exemplo:
Podemos multiplicar por 1 o número, e quando multiplicamos por 1, apenas somamos uma fila com a outra fila paralela, como exemplo:
