Matrizes - História, conceito e tipos

 Matrizes nada mais são do que tabelas com seus dados organizados para solução de problemas.

As matrizes são comumente representadas por:

[ ] - Colchetes, como mostra no exemplo da figura acima.

( ) - Parênteses.

||  || - 2 barras verticais.

As matrizes são compostas por linhas (fileiras horizontais) e colunas (fileiras verticais), e escritas com letras maiúsculas seguidas dos índices (numero de linha e numero de coluna), conforme figura abaixo:

A quantidade de linhas e colunas é o que define a ordem da matriz e suas informações são chamadas de elementos.

Um exemplo é o boletim de um aluno:

Os elementos desse boletim podem ser reescritos como matriz para pode realizar cálculos se necessário.

Podemos dizer que essa é uma matriz chamada B de Boletim de índice 6 x 3 logo:

Para identificar os elementos da matriz, escrevemos ele com letras minúsculas, seguidos  da posição desse elemento na linha  e depois na coluna, da seguinte forma:

A linha é representada por i e a coluna por j.

Por exemplo, utilizando nossa Matriz B do boletim:

Então o elemento na posição:

é  o 7 pois se encontra na quarta linha e segunda coluna.

TIPOS DE MATRIZES:

Matriz unitária:

São as matrizes que possuem apenas um elemento, exemplo:

A = [1]

Matriz Linha

São as matrizes que possuem apenas elementos em apenas uma linha, exemplo:

Matriz Coluna:

São as matrizes que possuem elementos em apenas uma coluna, exemplo:

Matriz Quadrada:

São as matrizes em que a quantidade de elementos na linha é igual a quantidade de elementos na coluna, exemplo:

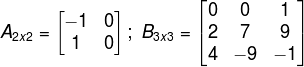
Nas matrizes quadrada temos as diagonais secundárias e principais, sendo: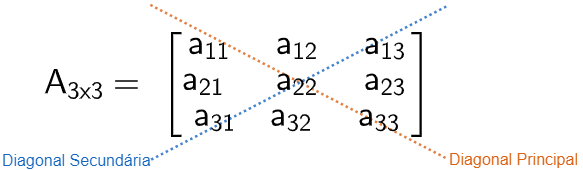

São tipos de Matrizes Quadradas: Matriz Identidade, Matriz Inversa, Matriz Singular, Matriz Simétrica, Matriz Positiva Definida e Matriz Negativa. Há também as matrizes transpostas e opostas.

Matriz Retângular:

São as matrizes em que a quantidade de elementos na linha é diferente da quantidade de elementos na coluna, exemplo:

Matriz Diagonal:

É uma matriz quadrada em que os elementos da diagonal principal são diferentes de zero (nulos), enquanto os demais são zero (nulos). Exemplo:

Matriz Identidade:

É uma matriz quadrada que possui todos os elementos da diagonal principal iguais a 1 e os demais elementos iguais a 0. Exemplo:

Matriz Oposta:

São matrizes que são geradas com valores oposto a uma determinada matriz, ou seja, e somente se, a_ij = -b_ij (valores negativos). Exemplo:

Matriz Transposta:

São matrizes que são geradas com a posição dos elementos invertidos quanto a uma determinada matriz, ou seja, a coluna de uma matriz é a linha de outra, assim como, a linha de uma matriz é a coluna de outra. Exemplo:

Matriz Nula:

São matrizes com os elementos nulos = igual a zero, exemplo:

HISTORIA DAS MATRIZES:

Segundo o site: http://www.mat.ufrgs.br

"Foi só há pouco mais de 150 anos que as matrizes tiveram sua importância detectada e sairam da sombra dos determinantes. O primeiro a lhes dar um nome parece ter sido Cauchy, 1826 : tableau ( = tabela ).

O nome matriz só veio com James Joseph Sylvester, 1850. Seu amigo Cayley, com sua famosa Memoir on the Theory of Matrices, 1858, divulgou esse nome e iniciou a demonstrar sua utilidade."

Usou o significado coloquial da palavra matriz, qual seja: local onde algo se gera ou cria. Com efeito, via-as como "...um bloco retangular de termos... o que não representa um determinante, mas é como se fosse uma MATRIZ a partir da qual podemos formar varios sistemas de determinantes, ao fixar um número p e escolhar à vontade p linhas e p colunas..." ( artigo publicado na Philosophical Magazine de 1850, pag 363-370 ).

Pierre Frédéric Sarrus (1798-1861) foi um matemático francês que inventou um método para o encontrar os determinantes das matrizes quadradas de ordem 3 (3x3) conhecido como a "Regra de Sarrus".

O "Teorema de Laplace", um método para calcular o determinante de qualquer tipo de matriz quadrada, foi inventado pelo matemático e físico francês Pierre Simon Marquis de Laplace (1749-1827).

A mãe da teoria das matrizes é a teoria das formas quadráticas, devidos aos seus métodos e resultados ser gerados por ela, hoje a teoria das formas quadráticas é apenas um capitulo da teoria das matrizes.

Vídeo:

atividade de matriz transposta  no geogebra: