Inequação Exponencial

 Uma inequação exponencial é quando a incógnita esta no expoente e temos na expressão um sinal de desigualdade.

E como se calcula uma inequação exponencial?

A inequação do segundo grau é calculada da mesma forma que as equações exponenciais. Basicamente igualamos a base, e como a base passa a ter o mesmo número, podemos passar o sinal de diferença dela para os expoentes, e assim calcular a inequação.

Vamos ao exemplo:

2^x < 2³

bases iguais, anulamos a base e o sinal da diferença passa para os expoentes:

x < 3

então a resposta é x é menor que 3.

S = {x ∈ ℝ\ x < 3}

Lê-se conjunto solução igual a x pertencente aos conjuntos dos  números reais tal que x é menor que 3.

No caso desse exemplo a base é maior do que 1, então o conjunto solução ali esta formado... mas e se a base for maior que 0 e menor que 1?

Nesse caso, devemos inverter o sinal da desigualdade da inequação original, como mostrado abaixo.

Vamos ao exemplo:

Por que inverte sinal?

Vamos lembrar que quando temos fração, podemos escreve-la como expoente negativo e incógnita negativa, deve ser multiplicada por -1 e assim, invertemos o sinal. 

Agora que entendemos a base, vamos aos cálculos....

 

Nesse caso, as bases são diferentes.... temos que fatorar a base ou as bases que necessitem ser reduzidas para que ambos os lados de desigualdade tenham o mesmo valor.

Nesse caso, 2 já é primo.. não precisamos fatorar.. mas podemos fatorar 32, logo:

Então:

Agora que ambas as bases são iguais, basta analisar se ela e maior que 1 ou maior que zero e menor que 1. Nesse caso é 2, que é maior que um, então, o sinal de desigualdade se mantem... basta apenas anularmos a base e encontrar o valor de x:

Então teremos:

x +  5 > 5

resolvendo a inequação:

x > 5 - 5

x > 0

logo montando gráfico temos:

Outro exemplo:

Vamos igualar as bases:

Observe que a base que era fracionária colocamos com expoente negativo. 

Observe também que temos expoente do expoente.... deixamos de fora o expoente já existente, para utilizar a propriedade das potências p3:

Logo teremos uma multiplicação do expoente da fatoração das bases com os expoentes já existentes:

Agora basta anular as bases e transformar os expoentes em inequação:

observe que como foi multiplicado por -1inverteu o sinal de diferente.

Logo, a resposta:

Mais um exemplo:

Vamos utilizar a propriedade P8 para transformar raiz em expoente e P6 para transformar fração em expoente negativa:

Agora anulando a base teremos a seguinte inequação com os expoentes:

Vamos ao último exemplo:

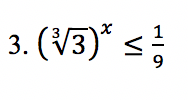
Nesse caso, podemos usar notação cientifica para escrever ou seja, colocar os números com base 10 elevado a alguma potencia....

Vamos la:

10 = 10¹

100 = 10² ou seja 10 . 10 = 100

1000 = 10³ ou seja 10 . 10 . 10 = 1000

Observe que conforme aumento um zero aumento em uma unidade meu expoente.... 

O mesmo ocorre se eu aumentar o zero a esquerda e adicionando virgula...

Prestaram atenção em um detalhe?? a quantidade de zero nos casos acima nos dão o valor do expoente da base 10? isso é só para titulo de curiosidade mesmo.

Então para resolver a inequação exponencial dada, precisamos colocar ambos os lados em base 10.

Para então podermos resolver:

Observe que poderíamos multiplicar o expoente do expoente, mas foi preferido transformar o expoente negativo de ambos os lados em fração.

Vídeo: