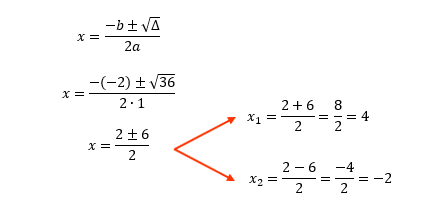Para resolver uma inequação do segundo grau, resolvemos da mesma forma da equação, através de Bháskara. E para encontrar o conjunto solução, devemos analisar o sinal da inequação.
Vamos ver na prática como fazer isso:
x² – 2x – 8 < 0
mudamos o sinal de desigualdade para igualdade, para que possamos calcular usando Bháskara.
x² – 2x – 8 = 0
a = 1 b=-2 c=-8
Δ = b2 – 4ac
Δ = (–2)2 – 4 ∙ 1 ∙ (– 8)
Δ = 4 + 32
Δ = 36
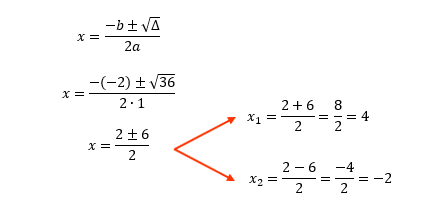
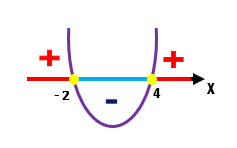
Observe que a é positivo, por isso a concavidade para cima.
Agora vamos usar a análise da desigualdade, observe que a inequação é menor que zero, com isso o conjunto solução será a parte negativa (menor que zero) do gráfico, sem levar em consideração o valor da raiz, pois o sinal é apenas de menor e não menor e igual... com isso, a bolinha das raízes não são preenchidas.
sendo o conjunto solução então:
S = {x ∈ ℝ | –2 < x < 4 }
Lê-se conjunto solução igual a x pertence ao conjunto do números reais, tal que, -2 é menor que x e x é menor que 4.
Outro exemplo:
–x² + 9 ≥ 0
a = -1 b=0 c=9
observe que o a é negativo, por isso a concavidade é para baixo.
agora analisando a inequação, temos que ela é maior e igual a 0, com isso pegaremos a parte positiva, e como é igual também a bolinha da raiz será pintada para incluir a raiz no conjunto solução.
Logo, o conjunto solução é:
S = {x ∈ ℝ | –3 ≤ x ≤ 3 }
Lê-se conjunto solução é igual a x pertencente ao conjunto dos números reais tal que -3 é menor e igual a x e x é menor e igual a 3.
outro exemplo:
2x² – 2x + 5 > 0
a=2 b=-2 c=5
Δ = b2 – 4ac
Δ = (–2)2 – 4 ∙ 2 ∙ 5
Δ = 4 – 40
Δ = –36 → Δ < 0
Como delta é negativo, não existem raízes reais, pois para conseguir extrair a raiz de números negativos, teríamos que utilizar os números complexos. Com isso, a parábola não toca o gráfico.
Como a é positivo a concavidade é voltada para cima.
Observe também que como qualquer valor que utilizamos para x o resultado da equação será sempre positiva, por isso, a parábola ficará acima do eixo x, ou seja o y será sempre positivo, veja alguns exemplos:
x = 2
2x² – 2x + 5 = y
2.2² - 2.2 + 5 = y
2.4 - 4 + 5 = y
8 - 4 + 5 = y
9 = y
x = -5
2.(-5)² - 2.(-5) + 5 = y
2.25 + 10 + 5 = y
50 + 10 + 5 = y
65 = y
Logo o gráfico ficará:
Agora analisando a inequação, temos que ela é maior que zero, ou seja vamos pegar a parte positiva.
Nesse caso, o conjunto solução será:
S = ℝ
outro exemplo:
–x² + 6x – 9 > 0
a=-1 b=6 c=-9
Δ = b2 – 4ac
Δ = 62 – 4 ∙ (–1) ∙ (– 9)
Δ = 36 – 36
Δ = 0
a negativo, concavidade para baixo, logo:
Agora, ao analisarmos a inequação ela dizia que é maior que zero, ou seja, o conjunto solução deveria ser o positivo, nesse caso como não existe, temos:
S = { } = ∅
vídeo:
atividade no geogebra: