Sobre os números complexos - forma geometrica - plano Argand-Gauss
A representação geométrica de um número complexo se da através do plano conhecido como plano complexo ou plano de Argand-Gauss. No plano, que é uma adaptação do plano cartesiano, o eixo horizontal é conhecido como eixo da parte real Re(z), já o eixo vertical é conhecido como eixo da parte imaginária Im(z).
O número complexo representado por a + bi gera os pontos no plano complexo formado pelo par ordenado (a, b).
Exemplo
Representação do número 3 + 2i na forma geométrica Z(3,2).
Os estudos sobre o plano complexo foram desenvolvidos pelos matemáticos Argand e Gauss, o que justifica seu nome e essa representação permitiu o desenvolvimento de vários conceitos, como o argumento de um número complexo, módulo de um número complexo, conjugado de um número complexo, entre outros.
A representação de um número complexo no plano cartesiano é conhecida também como afixo ou como imagem de um número complexo. Existem três casos de afixos:
- Imaginário qualquer, quando temos o número completo, onde as partes a e b são diferentes de zero, exemplo: 3 + 2i.
- Real, quando temos a parte imaginária igual a zero e a parte real diferente de zero, exemplo: 3.
- Imaginário puro, quando a parte real é igual a zero e a parte imaginária é diferente de zero, exemplo: 3i.
Modulo do Número Complexo
O módulo de um número complexo, geometricamente, é a distância do ponto (a,b) que representa esse número no plano complexo até a origem, ou seja, o ponto (0,0).
Como podemos perceber, |z| é a hipotenusa do triângulo retângulo, logo, ela pode ser calculada aplicando-se o teorema de Pitágoras, por isso temos que:
![]()
Exemplo:
Calcule o módulo do número complexo z = 3 – 4i.
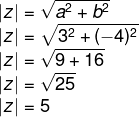
O argumento de um número complexo é o ângulo formado entre o eixo da parte real e o vetor OP.
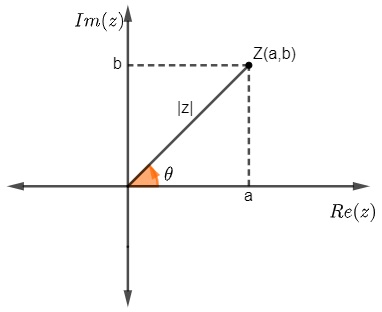
O cálculo do valor do argumento depende diretamente o valor do seno e do cosseno desse ângulo, logo, utilizamos as fórmulas:
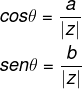
Exemplo:
Calcule o argumento de:![]()
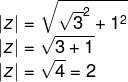
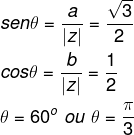
atividade geogebra:









