Relações de Girard - Soma e produto

 As relações de Girard consistem nas relações de soma e produto entre as raízes de uma equação. Ela foi criada por Albert Girard, que foi um matemático Belga que viveu entre 1590 a 1633.

Ele foi o matemático capaz de determinar as relações utilizando números negativos, o que por volta do século XVII não era aceito por muitos estudiosos.

As relações de Girard são baseadas em associar raízes de um polinômio com seus coeficientes e assim encontrar as raízes do polinômio estudado.

Como encontrar a relação em uma equação do segundo grau?

Como encontrar a relação em uma equação do terceiro grau?

Como encontrar a relação em uma equação de n graus?

Exemplo:

Vejamos as seguintes equações do segundo grau:

para a primeira equação:

r1 + r2 = -b/a

-4 + (-6) = -10/1

-4 - 6 = -10

-10 = -10

r1 . r2 = c/a

-4 . (-6) = 24/1

24 = 24

para a segunda equação:

r1 + r2 = -b/a

3 + (-1) = -(-2)/1

3 - 1 = 2/1

2 = 2

r1 . r2 = c/a

3 . (-1) = -3/1

-3 = -3

Mas de onde surgiu a fórmula?

Uma equação do 2º grau possui a seguinte lei de formação: ax² + bx + c = 0. As raízes dessa equação são dadas por x1 e x2. Veja: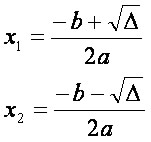



Determinando a soma das raízes:

Determinando o produto das raízes:

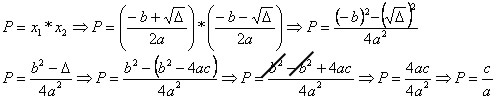
Para quem devemos usar as relações de Girard?

As relações são utilizadas antecipando o cálculo das raízes. Dessa forma, não precisamos determinar o valor do discriminante ao utilizar a fórmula de Bháskara. As expressões criadas por Girard oferecem a soma e o produto através somente dos valores dos coeficientes numéricos da equação do 2º grau.

Vídeo explicativo:

Vídeo de resolução de exercício do profmat