Operações com números complexos - Potencia e raiz

 Como os números complexos foram criados da necessidade de extrair raízes negativas, a operação de potência (inverso da raiz) e a própria raiz dessa classe de números se torna um pouco mais lógica.

Potência:

A figura acima mostra a tabela de resultado da potencia dos números imaginários. Note que os resultados se repetem de 4 em 4, logo, se dividirmos a potencia de i por 4 o resto pode ser a redução do expoente e assim facilitar a resolução.

exemplo:

Potência em forma polar (trigonométrica):

Para calcular a potência da forma polar, utilizamos a primeira fórmula de Moivre. 

Temos a forma polar dos números complexos sendo:

Agora imagina se elevarmos Z a potencia n, como fica:

Logo, se juntarmos toda a potencia de n ficamos com a seguinte fórmula:

Exemplo tirado do site: https://www.somatematica.com.br/emedio/complexos/complexos10.php

Calcule :

Vamos considerar  para posteriormente calcularmos . Para aplicar a 1ª fórmula de Moivre, precisamos calcular o módulo e o argumento de z.

Módulo: 

Argumento: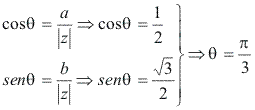 

Calculando :

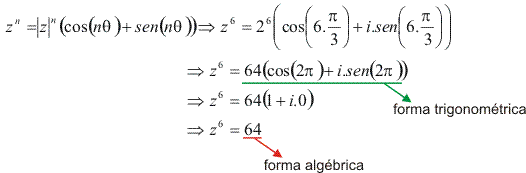
Raiz:

Sempre que nos deparamos com raiz enésima de i precisamos lembrar que a resposta será um número complexo. Então:

Para eliminar a raiz posso elevar ambos os lados do sinal de igual pela mesma potencia enésima, ou seja, passamos a raiz enésima para ou outro lado como forma de potencia:

ou seja: 

Podemos então separar a parte imaginaria e real de ambos os lados, e montar um sistema de equação para cada uma para localizar o valor de  a e b.

Exemplo:

de um lado do sinal de igual, sabendo que o formato do número complexo é parte real + parte imaginaria, temos:

parte real = 0

parte imaginaria = 1i 

do outro lado do sinal de igual temos:

parte real = a² - b²

parte imaginária = 2abi

igualando parte real com parte real e parte imaginaria com parte imaginária, teremos um sistema para encontrar os valores de a e b. Para isso deixaremos o i de lado.

a²- b² = 0

2ab = 1

resolvendo a primeira equação temos:

Na segunda equação podemos substituir b por a, por causa da igualdade acima logo teremos

2a.a = 1 ou 

2a² = 1

a² = 1/2

Vamos racionalizar para eliminar a raiz do denominador, multiplicando o numerador e o denominador pelo denominador:

se a = b e a raiz de i = a + bi logo

Se tiver um numero multiplicando o i basta fatorá-lo e extrair a raiz separadamente. Exemplo:

Raiz em forma polar (trigonométrica):

Para calcular a raiz em forma polar, usamos a segunda fórmula de Moivre.

Vamos lembrar do número complexo em sua forma polar: 

Podemos dizer que:

Nesse caso, o complexo u é chamado de raiz enésima de z.

Se Z tem a forma polar ja mencionada, U tem a seguinte forma polar:

se U esta em potencia de expoente n, aplicando a fórmula de potência dos números complexos em sua forma polar, temos:

comparando as partes onde temos:

e

Como n beta é o argumento de u, este deve pertencer ao intervalo [0; 2π[ ou [0; 360º[ .Logo:

Se então substituindo:

temos a fórmula de radiciação:

exemplo retirado do site: https://www.somatematica.com.br/emedio/complexos/complexos10.php

Exemplo

Determine as raízes cúbicas de z = 8.

Resolução

Vamos calcular o módulo e o argumento de z para a aplicação da 2ª fórmula de Moivre:

Módulo: 

Argumento: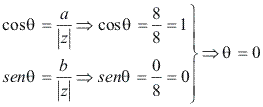 

As raízes cúbicas de 8 são dadas por:

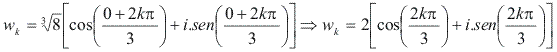
O número k pode assumir os valores 0, 1 e 2:

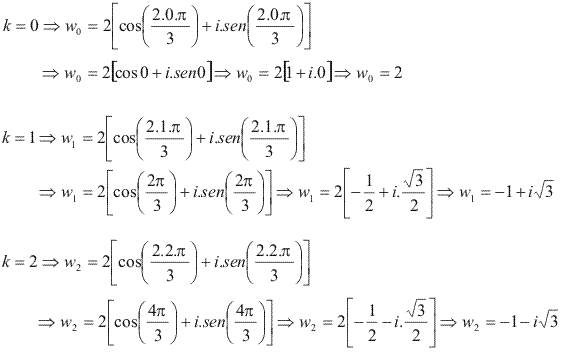
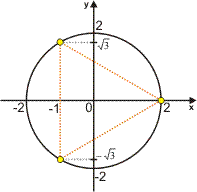
Geometricamente, note que as três raízes estão sobre uma circunferência de raio 2 e são vértices de um triângulo equilátero; seus argumentos formam uma PA, cujo primeiro termo é 0 e a razão é.

Vídeo potência:

Vídeo raiz:

Atividade geogebra de raízes de números complexos: