Razão trigonométrica
As razões trigonométricas, também conhecida como relação trigonométrica são os estudos das relações entre as medidas do triângulo e seus ângulos.
Além das razões mostradas na figura acima, ainda temos outras relações importantes:
Observando que 2 triângulos retângulos com o mesmo ângulo possuem semelhanças entre si, foi criada as razões trigonométricas. O seno de um ângulo é invariável independentemente da medida do lado do triângulo de onde esse ângulo foi tirado, devido a essa razão.
Um exemplo disso é o seno do ângulo de 30º onde temos as medidas:
Verificando todos os ângulos inteiros, foi possível obter os valor de seno, cosseno e tangente para todos os ângulos, gerando uma tabela com os valores, veja abaixo um exemplo:
atividade no geogebra:
Além das razões mostradas na figura acima, ainda temos outras relações importantes:
Observando que 2 triângulos retângulos com o mesmo ângulo possuem semelhanças entre si, foi criada as razões trigonométricas. O seno de um ângulo é invariável independentemente da medida do lado do triângulo de onde esse ângulo foi tirado, devido a essa razão.
Um exemplo disso é o seno do ângulo de 30º onde temos as medidas:
Calculando o seno temos:
Sen30º = Cateto oposto a θ = 2,31 = 0,5
Hipotenusa 4,62
Hipotenusa 4,62
O valor 0,5 é o seno de 30° para qualquer triângulo. Isso acontece porque todos os triângulos que possuem dois ângulos congruentes são proporcionais. Nesse exemplo, 0,5 é justamente a razão de proporção encontrada nos triângulos retângulos que possuem um ângulo de 30°.
Como resolver?
Calcule o valor do lado de comprimento a no triângulo seguinte: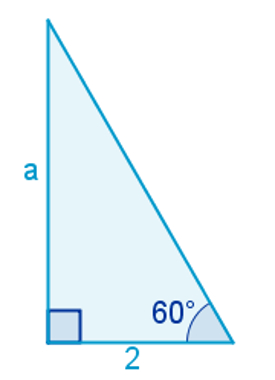
Como o que queremos calcular é o a que esta como cateto oposto, e temos o valor do cateto adjacente, a formula que traz esses 2 itens é o da tangente logo, com a fórmula em mãos, basta fazer a substituição:
Tg60 = Cateto oposto a 60 = a
Cateto adjacente a 60 2
Tg60 = a
2
1,732 = a
2
a = 1,732·2
a = 3,464
Você Sabia que:
As razões trigonométricas foram muito importantes para cálculos astronômicos desde muitos anos atrás, um exemplo disso foi que Aristarco sabia que quando a Lua exibia um quarto iluminada (crescente ou minguante) era possível desenhar o triângulo retângulo da figura, ele já conhecia a distância da terra e lua.
A distância B corresponde a que existe entre a Terra e a Lua, o ângulo A corresponde à separação angular entre a Lua e o Sol, visto por um observador na Terra. Então, para calcular a distância C, basta lembrar que ela é B dividida pelo cosseno do ângulo A; pois o cosseno de um ângulo é a medida do cateto adjacente a esse ângulo, no caso B, dividido pela hipotenusa do triângulo retângulo C.
Logo: Trigonometria elementar para calcular a distância da Terra ao Sol: cos A = B ÷ C logo C = B ÷ cos A.
Fonte: Costa, J. R. V. Aristarco de Samos e a distância Terra-Sol. Astronomia no Zênite, jul 2000.
Outra aplicação foi para descobrir o tamanho do nosso querido Planeta Terra.
Há cerca de 2200 anos atrás Eratostenes teve a seguinte ideia:
No solstício de verão do Hemisfério Norte, em Siena, ao meio-dia, o Sol ficava exatamente na vertical e sua luz se refletia na água de um poço profundo sem deixar sombras nas paredes. Porém, em Alexandria, uma cidade situada mais ao norte, naquele mesmo instante, o fenômeno não ocorria.
Então ele mediu o grau de inclinação dos raios solares (na figura indicado como luz do sol) com relação ao objeto estudado e a medida de sua sombra - percebam na figura q a sombra do objeto se torna o cateto oposto, o objeto se torna cateto adjacente e os raios solares hipotenusa de um triangulo retângulo. Ele deduziu q ao calcular o teta desse retângulo ele estaria encontrando o ângulo de curvatura da terra, pois os raios solares são emitidos em linha reta paralela.
Assim, ele encontrou o ângulo de 7,2 graus.
Sabendo que um circulo completo tem 360graus, ele dividiu 360 por 7,2 e obteve 50, ou seja, a distância entre Siena e Alexandria gerava um ângulo 50x menor q o ângulo total da terra... logo se multiplicasse a distância dessas 2 cidades por 50 ele teria o tamanho do nosso lindo planeta.
Pois bem a distância das cidades eram aproximadamente 800km, então 800 x 50 = 40.000 km se aproximando numero do tamanho real.
Pasmem, que a distância foi contada em passos q ele pagou para um caminhante contar entre uma cidade e outra.
Com mais exatidão, hoje sabemos que a terra possui uma circunferência de 40.075km.
O cara foi um gênio,
Não??
vídeo:
Relação fundamental da trigonometria:
atividade no geogebra:









