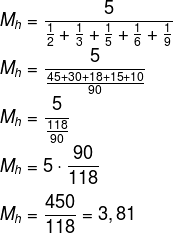Existem basicamente 4 tipos de média: aritmética, geométrica, harmônica e quadrática. Média significa no meio de; valor que está entre dois valores absolutos ou extremos.
A média aritmética, é a mais usada no nosso cotidiano, ela consiste em somar todos os números da lista e dividir pela quantidade de números somados tendo esses números peso ou não, com isso, ela é dividida em 2:
- Média aritmética simples: Na média aritmética simples não é considerado peso dos números no calculo.
Suponhamos que existam uma quantidade n de dados (x1, x2, x3, ..., xn) . A média entre esses dados será:
Exemplo: dado os números (2, 5, 7, 9, 12) qual é a média?
dado os números (4, 9, 13, 16, 19, 22, 27) qual é a média?
- Média aritmética ponderada: A média ponderada considera “pesos” para cada item, ou seja, em um conjunto de dados, cada item recebe uma importância. Vamos supor que tenhamos um conjunto com n dados (x1, x2, x3, ..., xn), onde cada dado receberá um peso, respectivamente (p1, p2, p3, ..., pn).
Cada item será multiplicado pelo seu peso. A média será dada pela divisão entre esta soma e a soma dos pesos considerados. A média entre esses dados será dada por:
Exemplo: Uma aluna fez um trabalho e obteve nota 9.0 com peso 2, outro trabalho, com nota 7,0 e peso 2, uma prova e obteve 8,0 e a prova tinha peso 3, uma participação de peso 1 ela tirou 8,0 e um debate de peso 1 tirou 3,0. Assim, a média dessa aluna será:
Média Geométrica: Como o próprio nome indica, a média geométrica sugere interpretações geométricas, por exemplo, podemos calcular o lado de um quadrado que possui a mesma área de um retângulo, usando a definição de média geométrica.
Ela é calculada como a raiz n-ésima do produto de n elementos de um conjunto de dados.
Exemplo: Qual é a média geográfica entre 2, 4 e 8?
Exemplo: Qual é a média geográfica entre os 2 lados desse retângulo?
Uma outra aplicação muito frequente é quando queremos determinar a média de valores que alteraram de forma contínua, muito usada em situações que envolvem finanças.
Exemplo: Um investimento rende no primeiro ano 5%, no segundo ano 7% e no terceiro ano 6%. Qual o rendimento médio desse investimento?
Para resolver esse problema devemos encontrar os fatores de crescimento.
1.º ano: rendimento de 5% → fator de crescimento de 1,05 (100% + 5% = 105%)
2.º ano: rendimento de 7% → fator de crescimento de 1,07 (100% + 7% = 107%)
3.º ano: rendimento de 6% → fator de crescimento de 1,06 (100% + 6% = 106%)
Para encontrar o rendimento médio devemos fazer:
1,05996 - 1 = 0,05996
Assim, o rendimento médio dessa aplicação, no período considerado, foi de aproximadamente 6%.
Média Harmônica: Quando trabalhamos com grandezas inversamente proporcionais, uma média interessante para a representação do conjunto de dados é a harmônica, que, junto à média aritmética e à média geométrica, é conhecida como média pitagórica.
Descrevemos a média harmônica como a quantidade de elementos no conjunto, divida pela soma do inverso dos elementos do conjunto.
Onde usar a média harmônica: a velocidade média, a vazão da água, a densidade, entre outras aplicações na física e na química. Algumas fórmulas da física, na verdade, surgem da média harmônica.
Exemplo, dado um conjunto A (2, 3, 5, 6, 9), como ele possui cinco elementos, a média harmônica de A é calculada por:
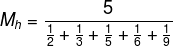
Para realizar a soma de frações, é necessário encontrar o mínimo múltiplo comum entre os denominadores:

O m.m.c (2, 3, 5, 6, 9) é igual a 90, logo, é possível realizar a soma das frações no denominador:
Média Quadrática: A raiz quadrada da média aritmética de uma quantidade finita de valores quadráticos é chamada média quadrática.
Exemplo: Média quadrática do conjunto

é dada por:



A média quadrática é muito utilizada para valores que variam entre positivos e negativos, como as ondas eletromagnéticas, sonoras, etc. Exemplos mais comuns: a energia eléctrica entregue ao consumidor por uma onda de Corrente Alternada (CA) e a potência dos aparelhos de som.
vídeo:
atividade geogebra:
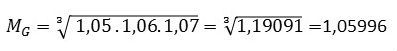
![]()